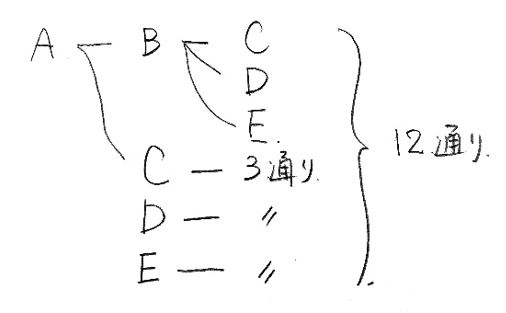
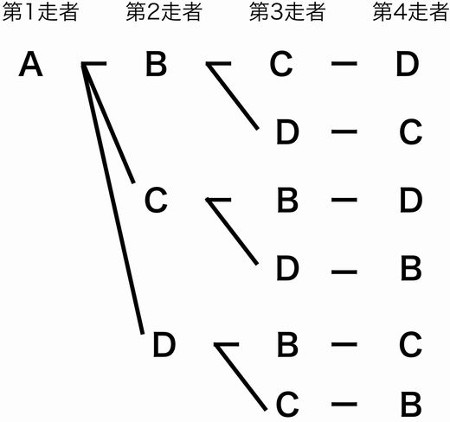
念のため2つの法則を確認しておきます。 和の法則 事柄A,Bが同時には起こらないとき,Aの起こり方が m 通り,Bの起こり方が n 通りとすると,AまたはBのどちらかが起こる場合の数は,( m n )通りである。 積の法則 事柄Aの起こり方が m 通りあり,その各々に対して事柄Bの起こり方が n 通りあるとき,AとBがともに起こる場合の数は( m × n )通りである 1 組合せの総数·····p1 2 ncr の性質·····p5 3 組合せの考え方の利用·····p7 4 組合せの総数·····p17 5 「順列」と「組合せ」の見分け方·····p21 6 同じものを含む順列·····p23 7 選ばれないものがある組合せ(重複編)·····p29 学年 高校1年生, 単元 場合の数, キーワード 順列つまり、順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ

順列の問題 一定の条件で並べる 高校数学の知識庫
順列 組み合わせ 見分け方
順列 組み合わせ 見分け方-順列と組み合わせの定義 順列とは、順序を持った並べ方。例えば、{1,2}と{2,1}は別のもの。 組み合わせは、順序を持たない並べ方。例えば、{1,2}と{2,1}は同じもの。 例題(順列・組み合わせの基本) 1から3までの数が書かれたカードを2回引きます。順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典 順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



辞書 順列 組合せの問題の見分け方 わかりmath
<考え方> 右図の4種類の座り方は,左上の座り方を回転させたものです このように「回転させれば一致する並び方は同じならび方とみなす」のが円順列です 円運列とは,座席を区別せず,ものの相対的な位置関係だけを区別するものだともいえます右図のどの場合にもAさんの右手にはB 順列と組み合わせの違い 順列と組み合わせの違いは、選び出した/取り出したものの 並び順を考慮するかどうか です。 「順列」は取り出したものの並び順を考慮しますが、「組み合わせ」では並び順を考慮しません。 順列の解き方(慣れるまでの解法) 順列の問題 では次に、「abcの三人の中から二人を選んで並べる」場合、何通りあるかを考えてみましょう。 順列の考え方 まず、二人を選ぶことだけを考えましょう。
順列 n P r n C r のように,順列をr!で割ると組合せになりますが,重複順列 n Π r と重複組合せ n H r の関係は単純ではありません これは,上の例のように重複組合せの中身ごとに並べ方の総数が変わり,倍率が一定のr!にならないからですならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。辞書順列・組合せの問題の見分け方|わかりmath 男子8人、女子6人がいるとき、次の方法は何通りあるか。 (1) 男子2人、女子2人の計4人を選ぶ方法。 (2) 男子、女子から少なくとも1人ずつの計4人を選ぶ方法。
って作成者は思いながら問題をつくるでしょう。 単純な問題での見分け方を書いておくと、 問題に、 「並べ方はいくつあるか」と聞かれれば順列、 「組み合わせは何通りあるか」と聞かれれば組み合わせ、 という単純なことです。 日本語の表現が変わることで分かりにくくしてありますが、 「順番や位置が関係する」場合は順列 、 「順番は関係しない」と1組としたものを、 n 個のものから r 個とった組合せといい、その総数は で求めます。 つまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では順列・組合せの問題の見分け方 を使ってみてね。 (1) これらの8文字を1列に並べる方法 (2) すべてのOとAが偶数番目にあるもの (3) Y、K、H、Mの4文字がこの順にあるもの(隣り合わなくてもよい)




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



場合の数 組合せについて 日々是鍛錬 ひびこれたんれん
Try IT(トライイット)の「場合の数」の数え方4(たし算・かけ算の見分け方)の映像授業ページです。 Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。場合の数と確率問題文の意味の取り方について 場合の数と確率排反事象と独立試行の違い 場合の数と確率組分けの問題の見分け方 場合の数と確率順列と組合せの見分け方 場合の数と確率条件つき確率の解き方について練習問題 順列と組合せの問題を混ぜました。 順列と組合せの違い 順列 :「選んで並べる」「ABとBA を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「ABとBAは区別せず同じもの」 に注意しながら,考えてみてください。 例題3 (1) 5




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com
確率の順列・組合せの中でも「重複組合せ」は教える側にも教わる側にもやっかいな問題ではある。 公式としては、 異なるn個から同じものを選ぶことを許して、r個選ぶ場合の数は、 で済んで(済ませて)しまうが、具体例での説明からこの公式への このうち、 {A、B、C}、 {A、C、B}、 {B、C、A}、 {B、A、C}、 {C、A、B}、 {C、B、A} は組み合わせ1つと考えます。 つまり、1つの組み合わせは の並べ方があることが分かります。 ですので、組み合わせの総数は・・ 10通りになることが分かります。 ここでもしかしてピンときたら鋭いですが、章1の「順列と組み合わせの違い」の「5人の中から2人を選ぶ組み合わせの数 5 枚から 3 枚を選ぶ組み合わせの総数 5 枚から 3 枚を選ぶ組み合わせの総数は 5C3 と表記できます。 ※ C は combination の略です 5C3 は 5 枚から 3 枚を選ぶ「順列」の総数 / 3 枚の「置換」の総数 のことです。 これは 5P3 / 3P3 で表せますね。 計算すると (5 * 4 * 3) / (3 * 2 * 1) で 10 になります。 よって 5 枚から 3 枚を選ぶ組み合わせの総数は 10 通りです。




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾
見分け方まとめ:順列、組合せ、円、重複、組分けの違い 順列、組み合わせ、円、重複、組分け。 これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列と組み合わせの概要・公式・違い 順列と組み合わせの計算方法は記事の後半に回して、まずは 順列と組み合わせとは何なのか、その2つの違い も含めて紹介します。 順列とは、いくつかのものを順序をつけて列に並べる 並べ方 の総数です。 組み合わせとは、いくつかの要素の集ま 順列「p」と組み合わせ「c」の使い分け|確率 iPadProを授業で活用していくので、明日からともよし塾が進化します モル計算、濃度計算などの問題解説 レベル




順列pと組み合わせcの違いと 簡単 な見分け方




順列と組み合わせの公式とその違い 問題付き 理系ラボ
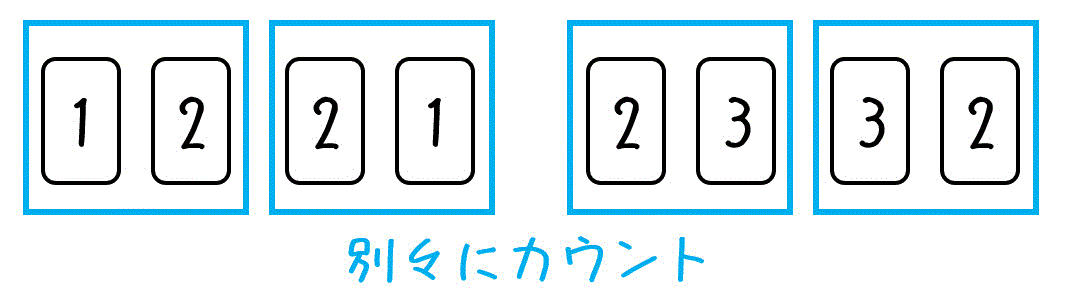
「順列」は「1列に並べる」「(順番を)区別する」 というのがポイントだったんだ。 一方、 組合せ とは、 異なるn個からr個を選ぶ ことだったね。 その場合の数は n C r で求めたよ。中学受験 5年 unit 71 場合の数1 順列と組み合わせ1 例題と解説 トレーニング 確認テスト ログインが必要です 関連する過去問 4年生向け 市川中学校06 場合の数順列と組み合わせの違いがよく分からない方は「順列と組み合わせの違いと"簡単"な見分け方」にて詳しく解説しています。 また、 「数学が苦手」「学校の授業が分からない」 そんな方にはスタディサプリがおすすめです。



3



3
攪乱順列(かくらんじゅんれつ)とは,その名の通り 数字の並びを完全にかくらんする(もとと同じ場所になる要素がない)順列 のことを表します。 例 n = 3 n=3 n = 3 の場合を考えてみる ( 1, 2, 3) (1,2,3) (1,2,3) を「かくらんする」順列を考える。 1番目が1でなく,2番目が2でなく,3番目が3でないのは ( 2, 3, 1) (2,3,1) (2,3,1) と初めに、その問題が順列なのか、組合せなのかを見分けます。 そのために、まず「順列」と「組合せ」とは何なのか考えてみましょう。 わかりmathでは、順列の問題を「 席の問題 」、 組合せの問題を「 組の問題 」と整理しています。 この2種類の問題では、それぞれ答えが変わってきます。 ①は順列で、答えは 5 p 2 =5×4=通り ②は組み合わせで、答えは 5 c 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。



辞書 順列 組合せの問題の見分け方 わかりmath




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
そこで今回は、順列と組み合わせの違いを解説し、場合の数の単元において多くの方を悩ませる、 「積の法則」と「和の法則」の考え方の違い をご紹介します。 コンテンツ 非表示 1 順列と組み合わせの違いは? 2 積の法則=各事象が同時に起こりうる高校数学の悩み―順列と組合せの違いが全然わからない! 高校数学の悩み―順列と組合せの違いが全然わからない! If playback doesn't begin 詳しくは順列・組合せの問題の見分け方のページを見てね。 積の法則 事象Aとなる場合が `n_A` 通りあり、 "Aが実際にどうなったかに関わらず" 、事象Bとなる場合が `n_B` 通りあるとき、事象A、Bがともに起こる場合は `n_A xx n_B` 通りある。




順列と組み合わせ 算数用語集




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書



100以上 順列 と 組み合わせ の 見分け 方 シモネタ



数学a 順列と組み合わせの違い 無料問題付き 平野雅人のブログ




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



辞書 順列 組合せの問題の見分け方 わかりmath




順列と組み合わせの公式とその違い 問題付き 理系ラボ



場合の数 順列と組み合わせの違いと並べ方問題の解き方



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




円順列 普通の順列との違いや公式を例題と共に工学博士が徹底解説 Rikeinvest




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組合せの違いと例題 高校数学の美しい物語
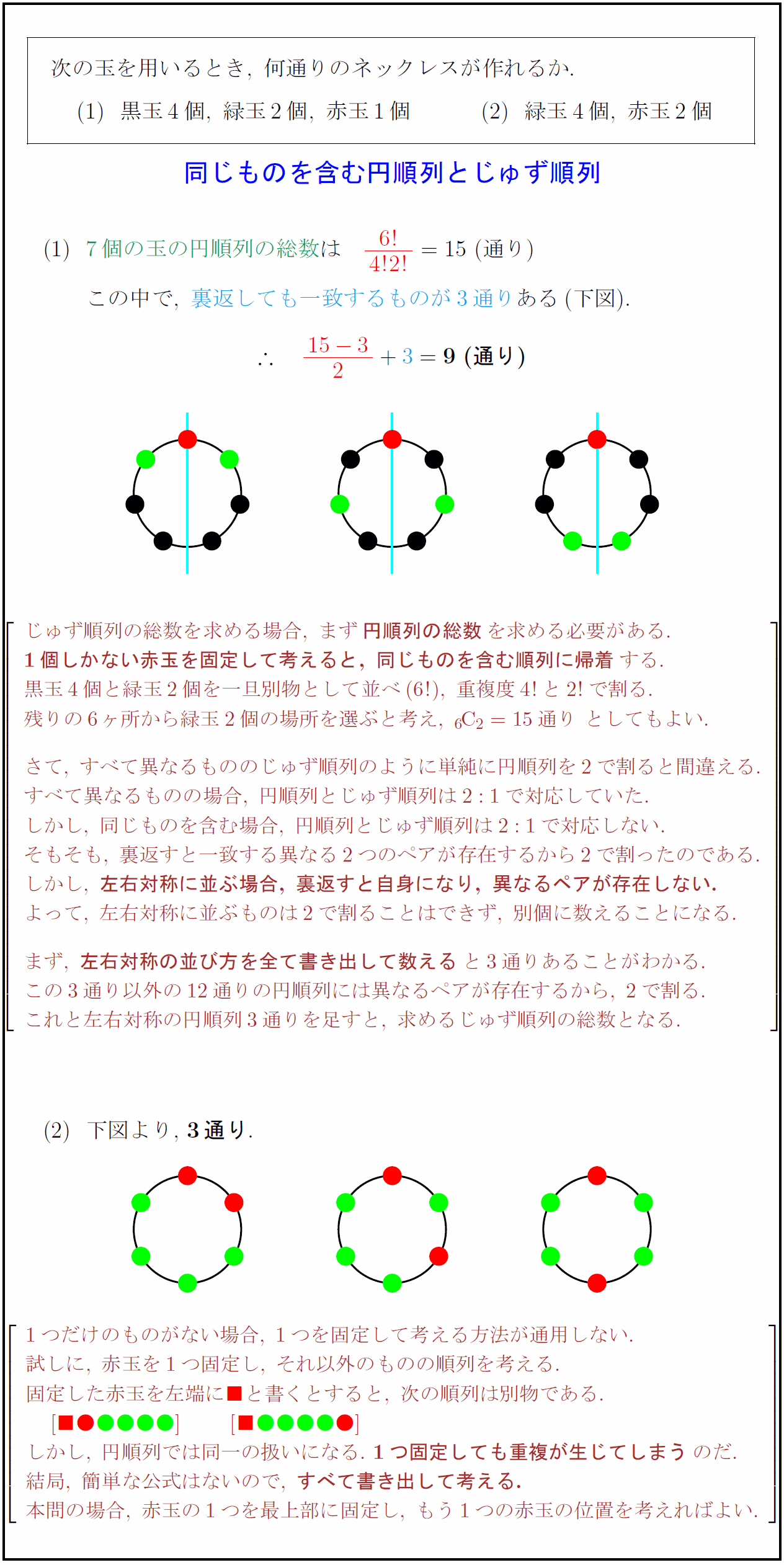



高校数学a 同じものを含む円順列とじゅず順列 受験の月




順列 p と組み合わせ c のちがい 数学a By Okボーイ マナペディア



順列 組合せ Pとcの違い 1 順列 ニャース滝の 猫が長靴をはいたなら



組み合わせ 計算 簡単




二項定理 二項定理のための 順列 組合せ 大人が学び直す数学



区別がない組分け 数学 苦手解決q A 進研ゼミ高校講座



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



数学 順列と組み合わせの見分け方を教えてください 順番にこだわ Yahoo 知恵袋




重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear



辞書 順列 組合せの問題の見分け方 わかりmath




こっちの方が早くないですか 一番の理由は組み合わせと順列の見分け 数学 教えて Goo




重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意




高校数学a 組合せの活用4 少なくとも 映像授業のtry It トライイット




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数の勉強方法 組み合わせと順列の解き方と勉強のコツ



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ




高校 数学a 場合の数31 pとcの違い 11分 Youtube



順列 組合せ Pとcの違い 3 ニャース滝の 猫が長靴をはいたなら



中学数学 場合の数




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ
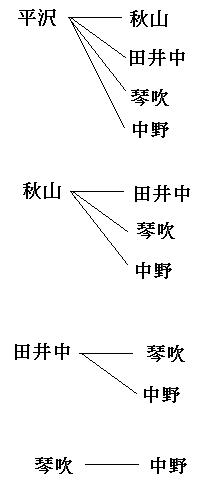



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
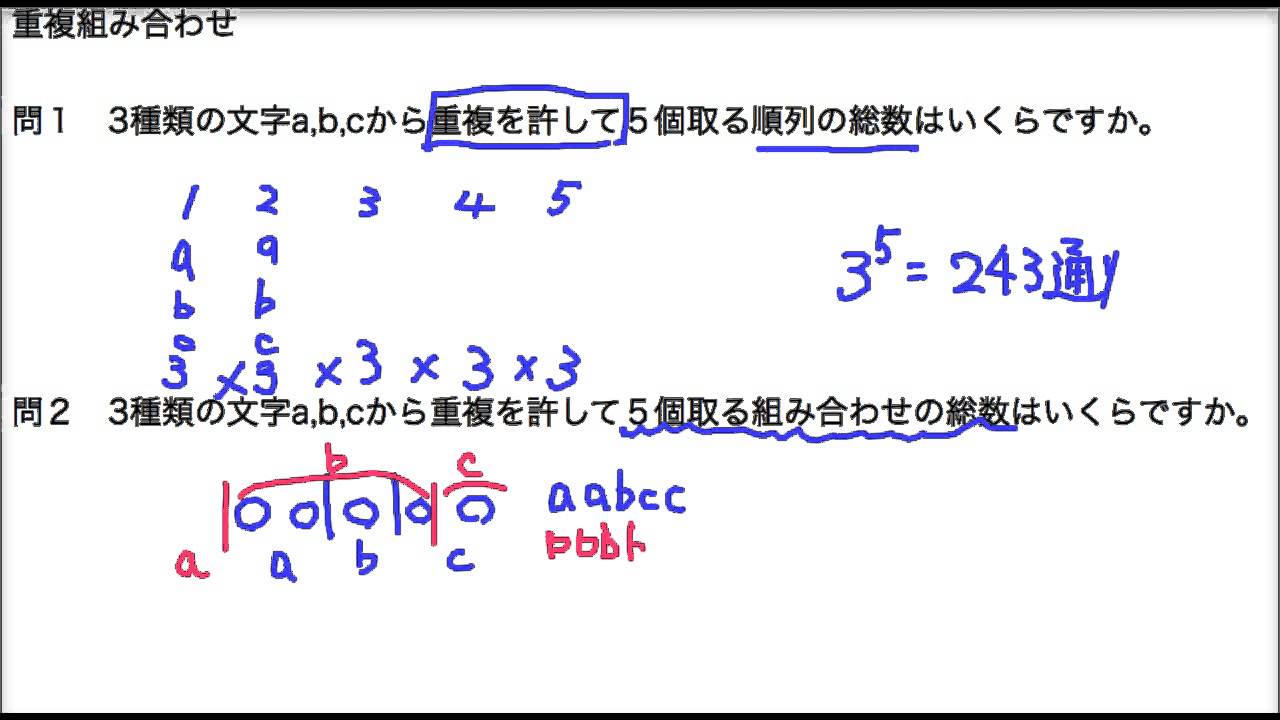



重複組み合わせ1 順列と組み合わせの違い Youtube




重複組み合わせ は2パターンを区別すればok




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




見分け方まとめ 順列 組合せ 円 重複 組分けの違い 理数白書



数学a 順列と組み合わせの違い 無料問題付き 平野雅人のブログ



3




数学 Npr 順列 の計算方法と意味




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ



数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com



数学a 順列と組み合わせの違い 無料問題付き 平野雅人のブログ




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clear
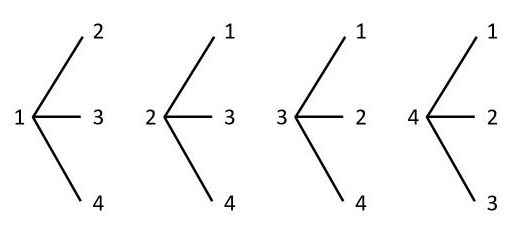



場合の数 順列と組合せ 和の法則と積の法則を正しく使い分けよう みみずく戦略室
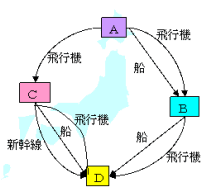



和の法則と積の法則の使い分け 数学 苦手解決q A 進研ゼミ高校講座



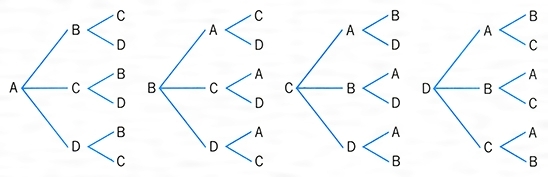
組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典



順列 組合せとは コトバンク



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear




順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング



3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com




高校数学a Npr と Ncr の使い分け 映像授業のtry It トライイット



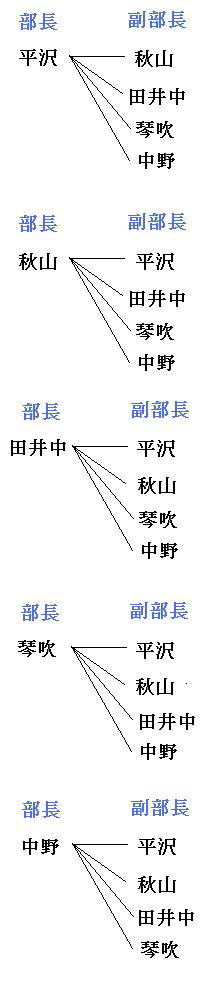
順列と組み合わせの違いをリレーのチーム選考に例える コード7区



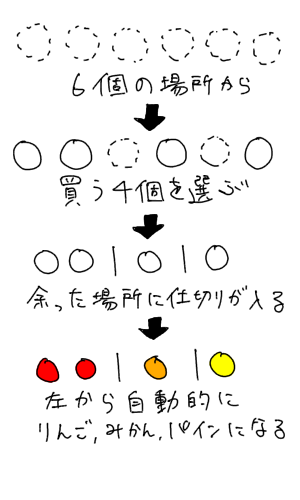
重複組合せ



重複順列と重複組合せの見分け方がわかりません6個の球をa B Yahoo 知恵袋



重複順列と重複組み合わせの違いについて教えてください ハンバーグ好きです Yahoo 知恵袋



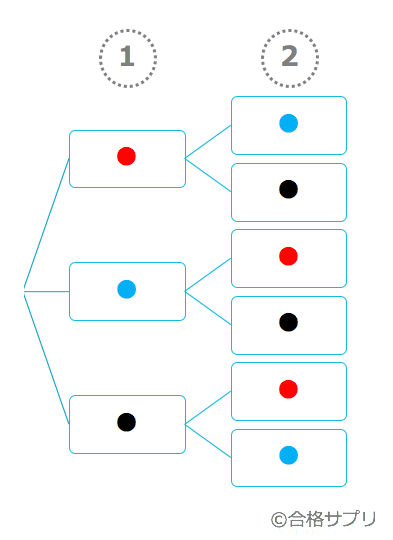
重複組み合わせは絵を描けば理解できる イラストで解説 理数白書




公式 組み合わせと順列の違い 見分け方 重複度を使う計算方法




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




順列の問題 一定の条件で並べる 高校数学の知識庫




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




公式 組み合わせと順列の違い 見分け方 重複度を使う計算方法



場合の数 順列と組み合わせの違い 中学受験プロ講師ブログ




順列pと組み合わせcの違いと 簡単 な見分け方




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々



Chiba




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b



1



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列pと組み合わせcの違いと 簡単 な見分け方



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ



0 件のコメント:
コメントを投稿