モールの応力円の描き方(2)モールの応力円の描き方(2) ((σ x σ y)/2, 0)を中心とし,先に プロットした両点を通る円を描 く. ((σ x σ y)/2, 0)を中心とし,先に プロットした両点を通る円を描 く. 必要であれば,主応力や最大せ ん断応力を求める. 実は単位円の考え方は三角比の範囲で少しやったことがあります。 どういうものだったかというと、まず座標平面上で半径が 1 の円である単位円を考えます。 この円上の点を一つとって原点と結びます。 この時 \(x\) 軸から測った角度(動径のところでやりましたね)を \(\theta\) とするとこ扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 この
円と三角形 角度 中学から数学だいすき
円 角度 求め方
円 角度 求め方- この記事では、三角関数について、角度の求め方や変換公式(\(90^\circ − \theta\) など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね! 目次 三角関数の下準備 単位円を知る; 半径1の円(「単位円」)の円周上の点$(x, y)$がx軸の正方向と角度$\theta$をなすとき、その座標は$(\cos\theta, \sin\theta)$で表されます。 図001 ️三角関数のsinとcos 高校の数学で、三角関数は直角三角形の辺の比で習ったという方も多いでしょう。それはもう忘れて




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
円の角度の求め方を教えてください。半径 Yahoo!知恵袋 円の角度の求め方を教えてください。半径343.5cmで円弧の長さが1cmの時、中心角は何度になりますか。よろしくお願いします。 円周率を314とします。また計算の便宜上、1の位は四捨五入しています 角度の求め方(第1 回 円のまわりをまわる円 算数の教え上手 面積の求め方(第5回) 算数の教え上手 面積の求め方(第3回) 算数の教え上手 面積の求め方(第2回) 算数の教え上手 面積の求め方(第1回) 算数の教え上手 面積の考え方(第2円の直径が角目目盛で10なら、その円からは1辺が10cmの正方形がとれることになります。 (画像の場合7cm) 2丸目の使い方 丸目は円状のものの円周が計算せずとも測れます。円の直径が丸目目盛で10なら、その円の円周は10cmだと分かることになります
円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば が得られます。 4まとめ 上記の1から3より接弦定理が成り立つことが示されました。 逆に、接弦定理 おうぎ形の弧の長さ = 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 弧の面積 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 角度別に分かるその証明方法 18年8月9日 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。
右図において,緑で示した2つの角は,一つの弧 に対する円周角だから等しい. ∠ ABE=60° また, ∠ AEB は ∠ BEC の補角だから ∠ AEB=180°−110°=70° 次に,三角形の内角の和は180°だから100円から読める!ネット不要!印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のPDF版の学習記事 三角関数の角度は?求め方 三角関数の角度は「三角関数の逆関数」で算定できます。三角関数の逆円弧の長さr、角度α、円周の長さ2πr、円の角度360°の関係は下記です。 r:2πr=α:360 α=360r/2πr=180/π=573(※π=314) ここで注目すべきは、弧度αは半径rの大きさに関係なく一定であることです。 弧度の読み方 弧度は「こど」と読みます。関係用語の読み方は下記が参考になり




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



円と三角形 角度 中学から数学だいすき
弧の長さ、弦の長さの求め方、長さの比較、弧や弦が等しいなら円周角も等しいことの証明などを整理しました。 算数から高度な数学まで、網羅的に解説したサイト 弧の長さと弦の長さの求め方、円周角との関係など 具体例で学ぶ数学 > 図形 > 弧の長さと弦の長さの求め方、円周角との関係解説 例題 6 右図のように同じ大きさの円がそれぞれの円の中心を通るように重なっています。 このときアの角度を求めなさい。 点P , Qは円の中心です。 解説 例題 7 右図のように正方形があり、その中に正方形の一辺を半径とするおうぎ形が2つありと求めてやることができます。 内角の和が求まれば 1つ分の大きさを求めることは簡単です。 外角のときと同じように割ってやればいいですね。 正三角形なら $$\LARGE{180 \div 3 = 60°}$$ 正五角形なら $$\LARGE{540 \div 5 =108°}$$ となります。 外角を利用した考え方




角度の求め方 算数の教え上手 学びの場 Com




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ
便宜的に元の円は点Oを中心とする半径1の円と定義して説明します。 まず、点AのY座標 (y₁)を sinθ から求める。円周の求め方 公式と計算例 円周の長さを求める公式は、次の通りです。 l = πd = 2πr l = π d = 2 π r 直径d、半径 r の円 ここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになり 速度・加速度の求め方 │ 受験メモ 図解でわかる円運動を東大院生が解説! 速度・加速度の求め方 高校物理の円運動では、 速度の公式、加速度の公式などなど、 色々と覚える公式が出てきます。 しかし円運動をきっちり理解できている受験生は




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




円周角 Wikipedia
※弧の曲線は円の一部分なので、弧の巾Wと高さhはどの部分を切り出して計算しても、Rサイズは同じです。 ※計算の正否が心配な場合は、弧の箇所(巾と高さ)を変えて計算してみてください。 上の図のテーブルの場合、 透明マットをオーダーするときのサイズは、 長辺1800mm 、短辺900mm ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線 焦点・接線や面積の求め方なども説明していくので、ぜひこの記事を通してマスターしてくださいね! 目次 楕円とは? 楕円の方程式とグラフ;




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生
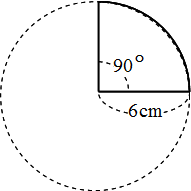



世界一やさしい 円の面積を求める問題の解き方 働きアリ
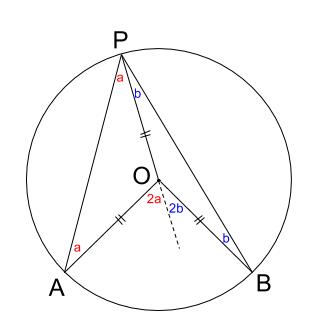
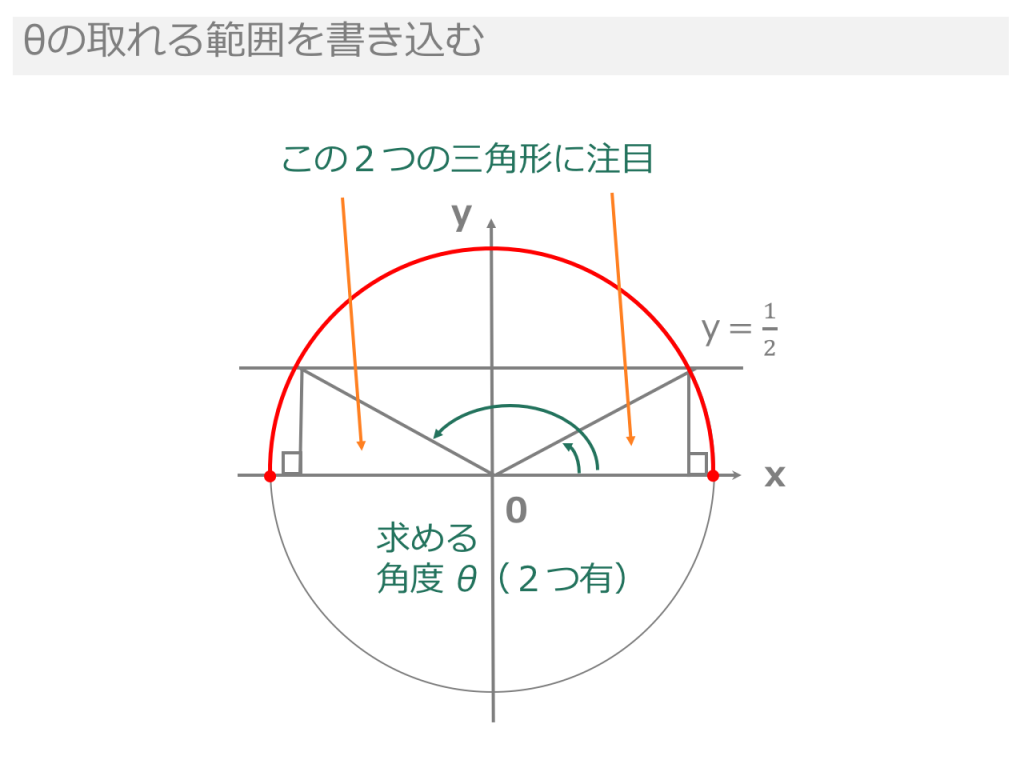
以上をまとめると三角方程式の解き方は「 単位円 を描き、 y=aの直線 を加えて、 三角形の比 を求めて角度を求め、 範囲を確認 して当てはまるもののみ答える」となります。 また、三角形の比は有名角のもの(30°、45°、60°など)に限られます。中途半端な外心の角度の関係 その1 ABCの外心Oをとして、外心O が ABCの内部にあるとき、外 接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわっの円曲線によって接続する基本的な曲線を「単曲線」と呼ぶ。単曲線は、コンパスで描く単純な円 の一部、つまり円弧となる。 以下に挙げる特定角度の三角比は、ぜひ覚えておきたい。 ※ 三角比で求める事のできない三角関数の場合は、問題に添付されている三角関数表から求める。 ※ �



円周角の定理を使った角度の求め方 写真の問題なんですが適当に書きま Yahoo 知恵袋




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi
まずbの角度から求めていきます。向かい合った角、つまり対頂角は等しいので、b=30° 次にaの角度を求めます。直線の角の大きさは180°です。そのためaの角度は、180°30°=150° cの角度は対頂角よりaと等しいので、c=150° よって、 答え a=150°、b=30°、c②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を説明し、 お子さんに作らせて、 気づいたこと外心とは、外接円の中心。 内心とは、内接円の中心。 重心とは、中線が交わる点。 では、それぞれどんな特徴があるのか確認しておきましょう。 Contents 外心の特徴、問題の解き方;
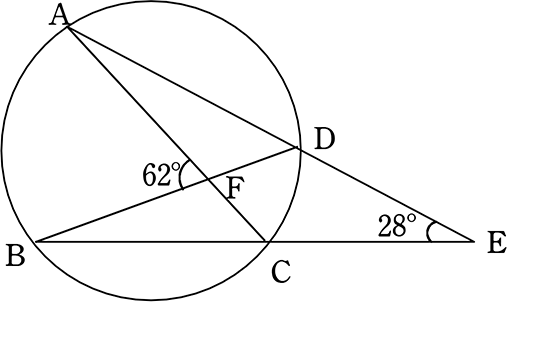



中学数学 円周角 中心角
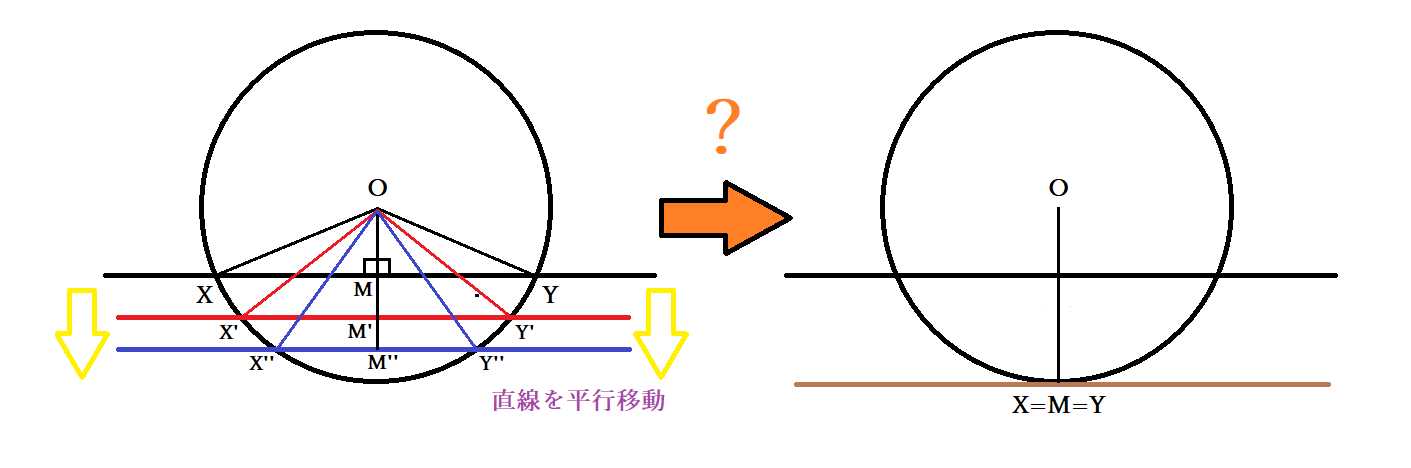



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐ピラミッド Googleマップで自宅・国立競技場間の距離を測って、このサイトで角度を求めました。度ぐらいとわかりました。 コンパスで方位もわかっているので、どのあたりに五輪のスモークが見れるのか、あたりがつきました。当日が




円周角の定理です Xの角度の求め方を教えてください Clear



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事3(2)a)の考え方で のように切り出すと、 と解くことができます。 (ただし、正弦定理で"角度"を求めると、次の答案のように解が2つ出てくることがあります。そのとき、2つとも解であることも、1つだけが解で他方は解でないこともあります。




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学
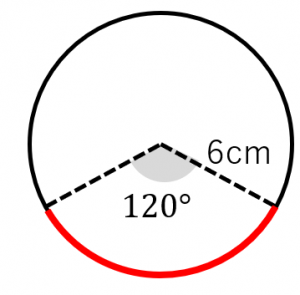



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
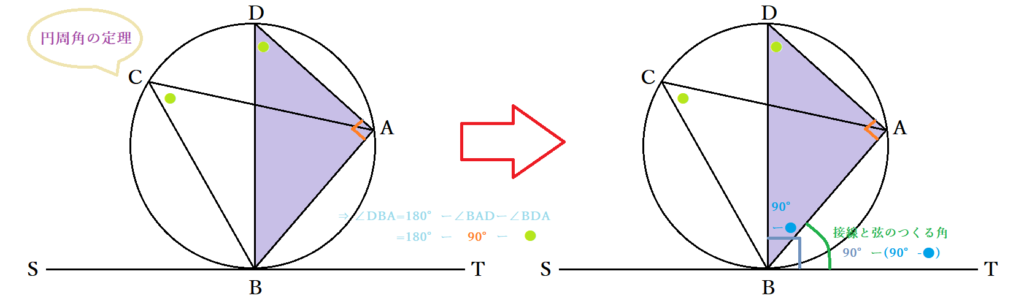



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog




Xの角度の求め方を教えて下さい Clear




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス
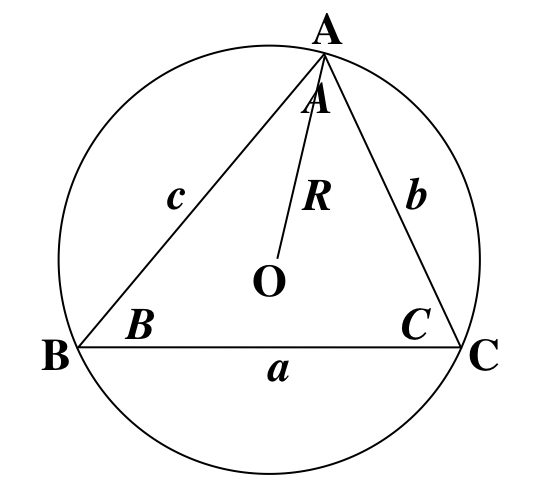



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



円周角




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理 角度の計算 中学数学 Youtube




角度の求め方を教えてください ちなみに答えは です お願いします Clear




円の中にある二つある三角形の角度の求め方 Okwave



1



1
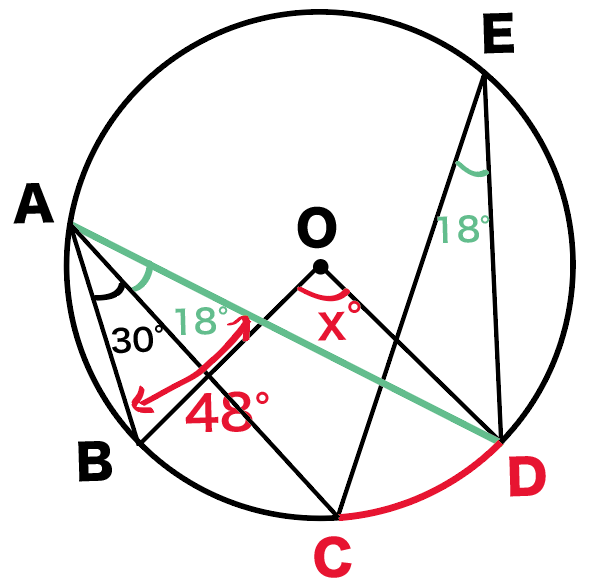



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



角運動の並進速度 接線加速度 求心 向心 加速度の求め方 陸上競技の理論と実践 Sprint Conditioning




接線と円の関係 Jsciencer




円周率pが現われる世界 3 Pが角度180 ってどういう意味 研究員の眼 ハフポスト




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd



円と三角形 角度 中学から数学だいすき



1




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
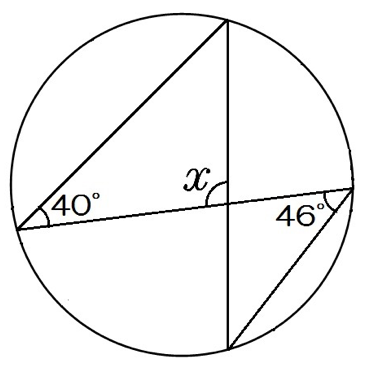



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




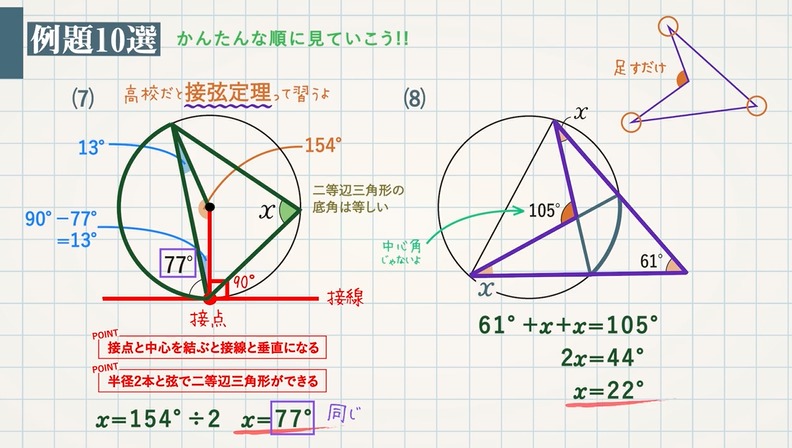
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
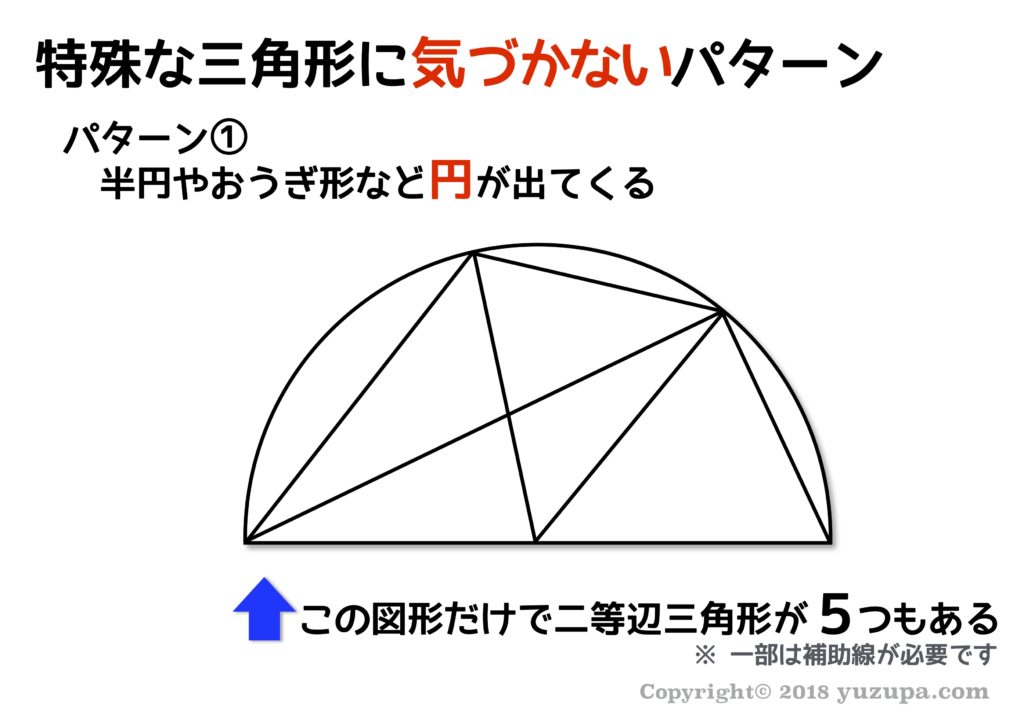



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




扇形の弧の長さの求め方 公式と計算例




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



1




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
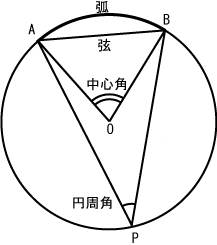



弧 幾何学 Wikipedia




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear
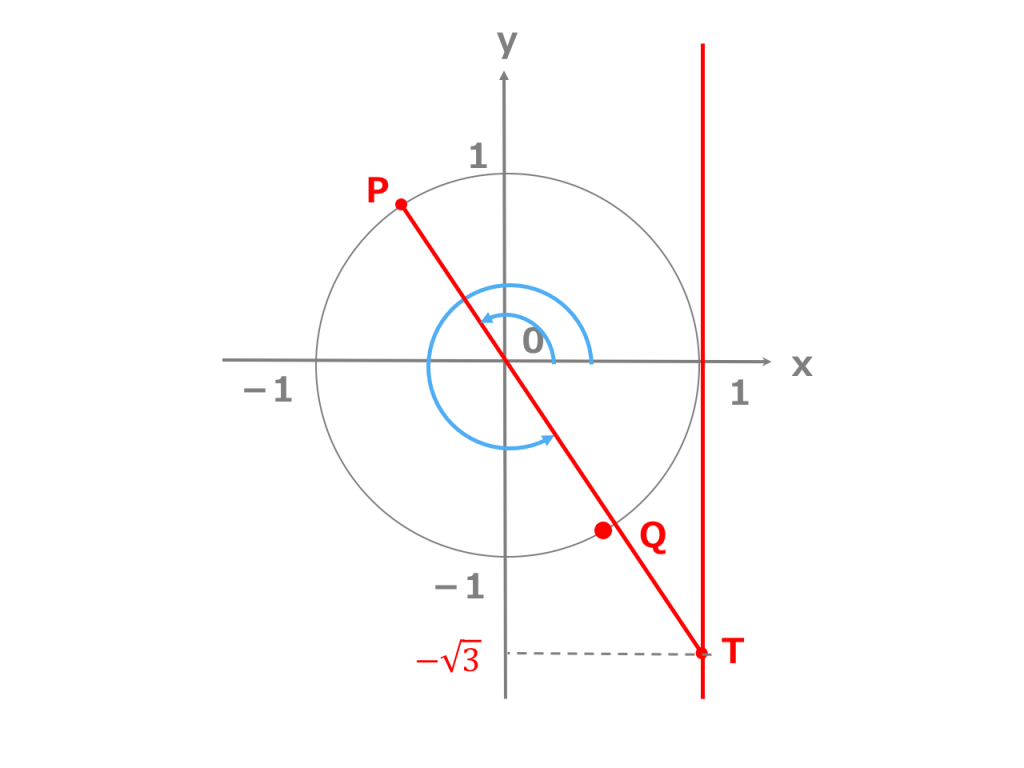



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su



円周角




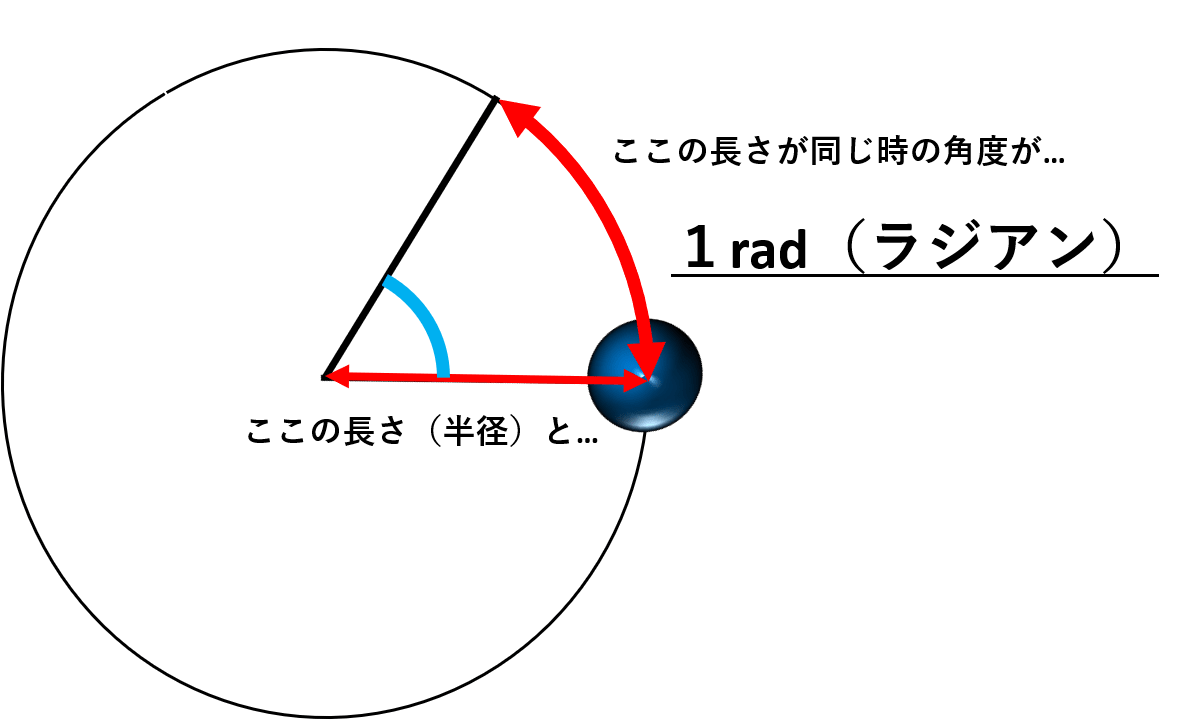
ラジアン 弧度法 の意味と 度 への変換方法




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




アルゴリズム 自由処



中3数学角度円周角 下の写真のxの求め方を分かりやすく教えて頂きたいです Yahoo 知恵袋
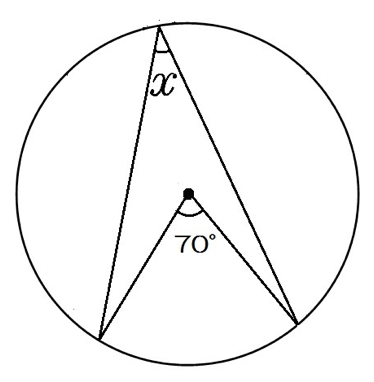



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円の接線と角度 中学から数学だいすき




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
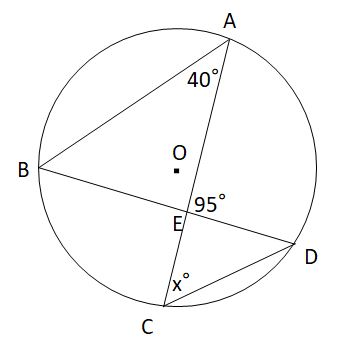



中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
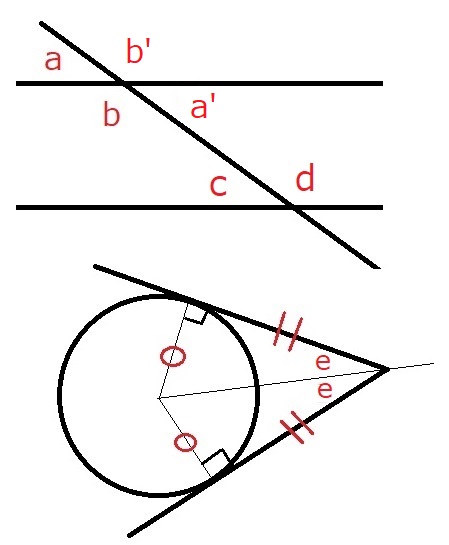



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
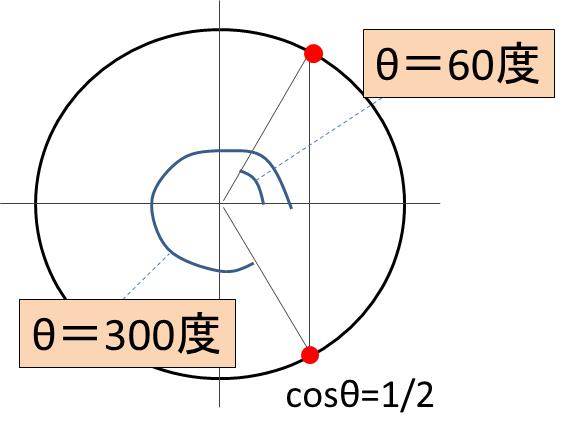



Cos8 1 2の角度 8の値 は Cos8 ルート3 2やcos8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム
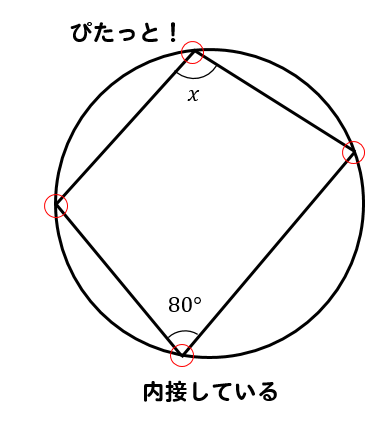



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



円周角の定理と中心角 中学3年数学 Youtube



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典




数学 中3 57 円周角の定理 少し応用編 Youtube



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係
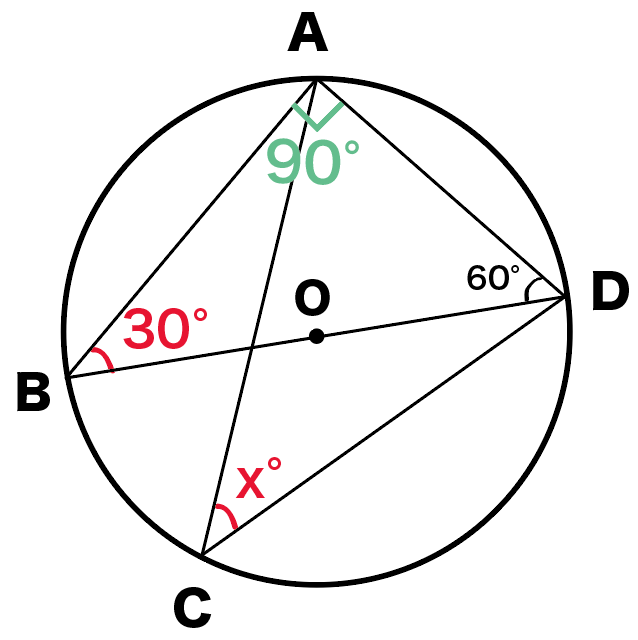



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
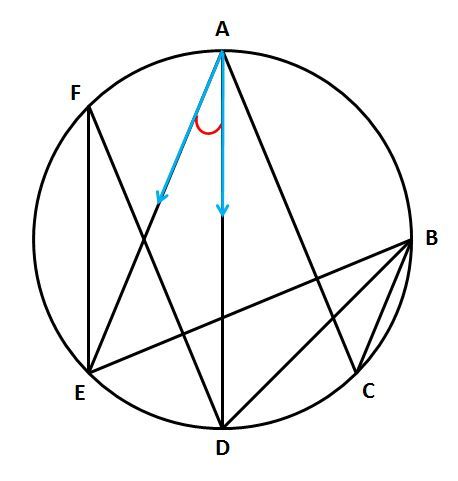



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



外接円 外心について
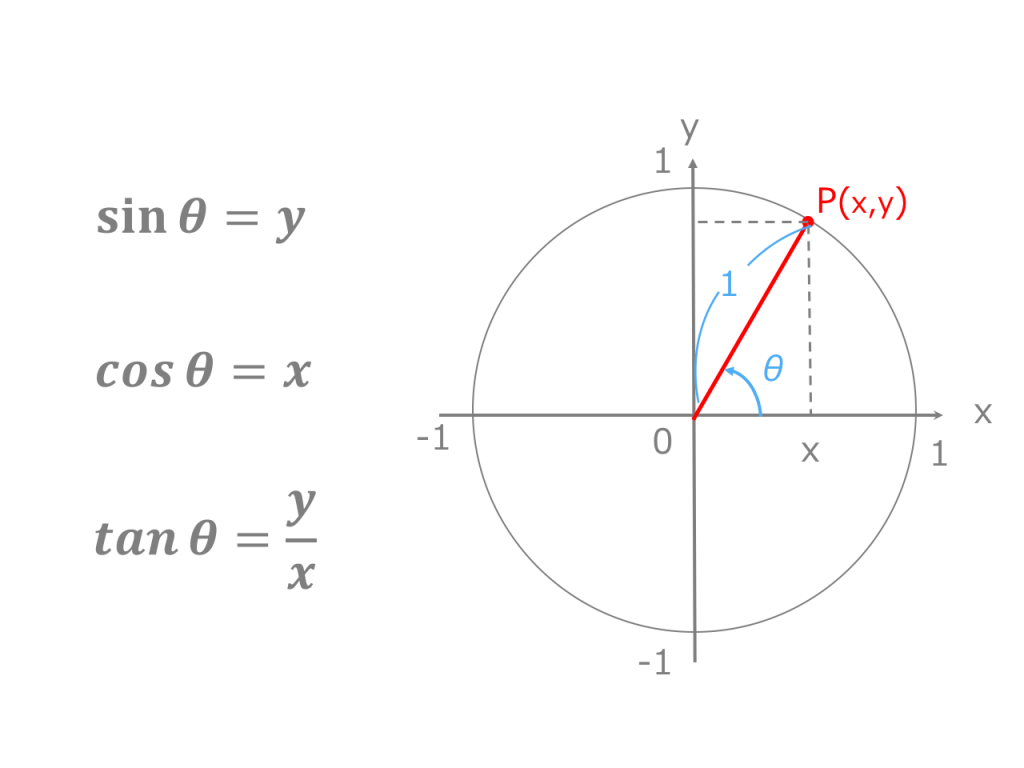



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



三角関数とは 1分でわかる意味 公式と計算 角度と値の関係




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
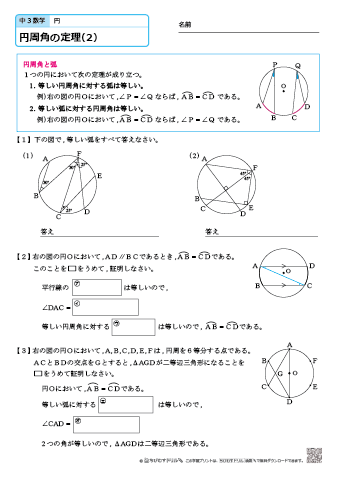



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



内接円 内心
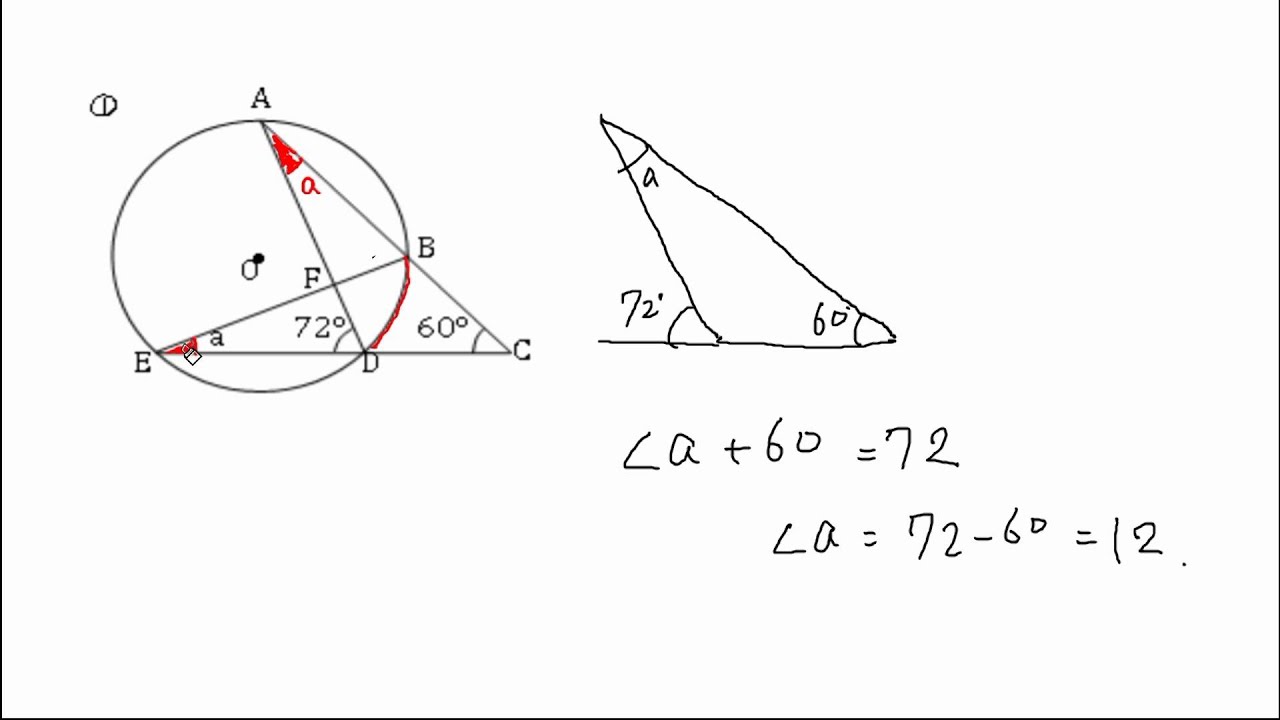



円周角の定理 問題 Youtube




円の中心からの角度から真円の円周上の座標を計算する Gamesprit




ちょうちょ型図形の角度は 求め方を徹底解説 数スタ



プチコン講座 角度計算の基本 ラジアン 三角関数




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



円周角




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
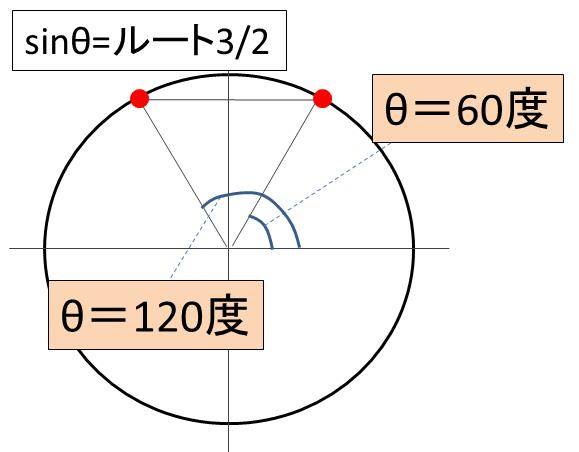



Sin8 1 2の角度 8の値 は Sin8 ルート3 2やsin8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム
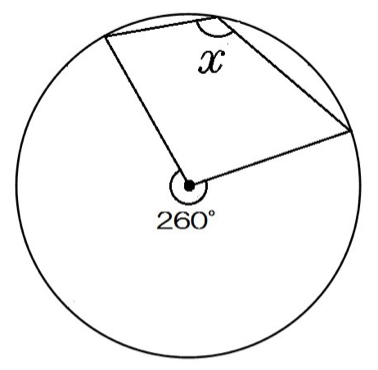



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




数学 中3 56 円周角の定理 基本編 Youtube
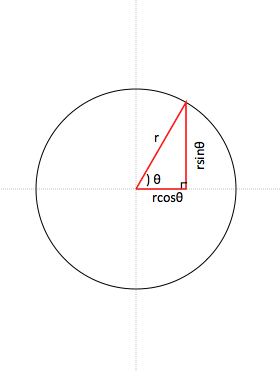



円の中心からの角度から真円の円周上の座標を計算する Gamesprit



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
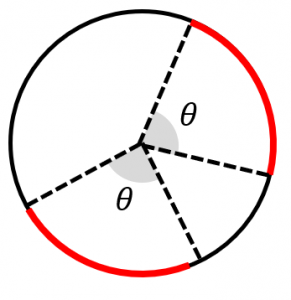



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
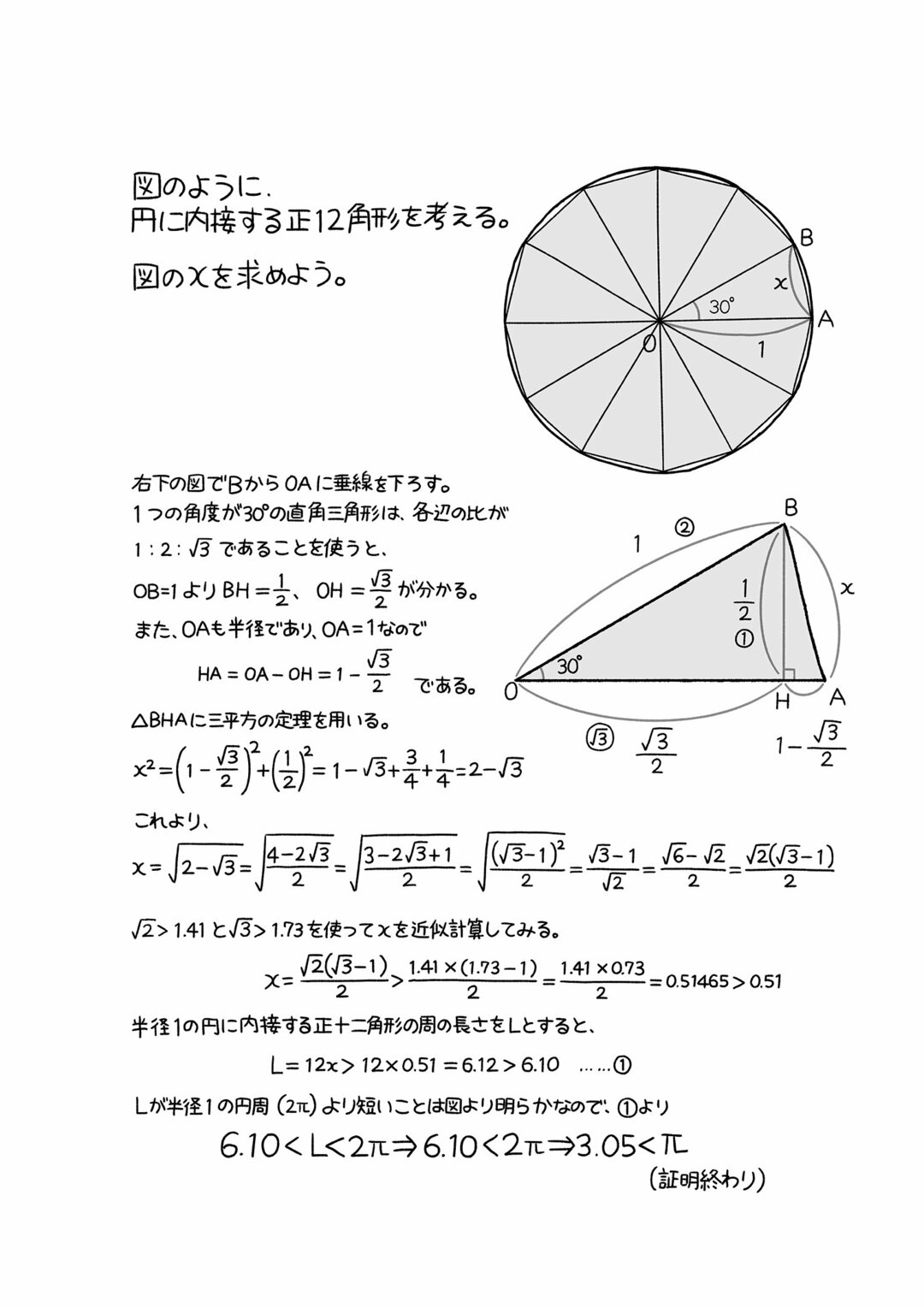



東大入試の有名問題 から円周率を探求する とてつもない数学 ダイヤモンド オンライン




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




角度の求め方 角度の求め方 Mqttk



0 件のコメント:
コメントを投稿