👍 Correct answer to the question Will mark brainliest Add 2√2 5√3 and √2 – 3√3 eeduanswerscom2/5–3/7 =(14–15)/35 =1/35, AnsAns yes we can add √8=√(2×2×2)=2×√2=2^1×2^(1÷2)=2^(3÷2)=2^15 Therefore √2√8=2^52^15=2^2=4ANSWER Explanation √x=x^(1÷2)square root of x Cube root of x= x^(1÷3) Similarly " n" th root of x= x^(1÷n) Note1) surds and exponential are int

Add 2 3 Root 7 1 2 Root 2 6 Root 11 And 1 3 Root 7 3 2 Root 2 Root 11 Brainly In
Add 2/21+3/7
Add 2/21+3/7-1 √−36 √√2 −12 3 −18−2√−12 4 √−813𝑖 √5 3−274√−48 6 √−49√−64−√−25 7 √−642√−16 √ 8 −128 9 State if each of the following numbers is rational, irrational, or imaginary a) √−25 √ b) √100 √c) d) 3−8 e) 360 10 What is the value of 2𝑖8?Click here👆to get an answer to your question ️ Add (2√(2) 5√(3) 7√(5)) and (3√(3) √(2) √(5))



What Is 2 5 3 7
Let's try to understand how do we add any two things let's say you have two flowers and your boyfriend gave you three more flowers, so now you have five flower in total you can see that in the given picture and blow that is a algebric representatiThe rationalizing factor of 2√3 is √3 2√3 × √3 = 2 × 3 = 6 Rationalize the Denominator Meaning Rationalizing the denominator means the process of moving a root, for instance, a cube root or a square root from the bottom of a fraction to the top of the fraction Rationalising Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) You are here Divide 5√11 by 3√33 Multiply 2√15 by 7√5 Simplify (√5√7)^2
Add 2√2 5√3 and √2 3√3 2 See answers kadamaryan2121 is waiting for your help Add your answer and earn points1 vote and 5 comments so far on RedditSteps for Solving Linear Equation \frac { x2 } { 3x } \frac { x2 } { 2x } =3 3 x x 2 2 x x − 2 = 3 Variable x cannot be equal to 0 since division by zero is not defined Multiply both sides of the equation by 6x, the least common multiple of 3x,2x Variable x cannot be equal to 0 since division by zero is not defined
1 / 73√2 = 1 / 73√2 x 73√2 / 73√2 = 73√2 / 4918 = 73√2 / 31 So, when the denominator of an expression contains a term with a square root (or a number under a radical sign), the process of converting it to an equivalent expression whose denominator is a rational number is called rationalizing the denominator Ex 2 √(50) = √(25 x 2) = √(5 x 5 x 2) = 5√(2) Though 50 is not a perfect square, 25 is a factor of 50 (because it divides evenly into the number) and is a perfect square You can break 25 down into its factors, 5 x 5, and move one 5 outAdding fractional exponents is done by calculating each exponent separately and then adding a n/m b k/j Example 4 3 3/2 2 5/2 = √ (3 3) √ (2 5) = √ (27) √ (32) = 5196 5657 = How to add fractional exponents with same bases and same fractional exponents?



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Prove That The Following Are Irrational I 1 2 Ii 7 5 Iii 6 2
2 Can √ 5 be simplified ?We take (2√3) = a equation (2√3) = b equation In a equation we take 2 and Multiply by equation b * (2)×(2√3) Then we multiply 2 by 2 and then 2 by √3 " in above equation" * 2×2 = 4 * 2×√3 = 2√3 Then we add the above equation (2 √ 6 √ 3)/ ( √ 6 √ 3) Add the fractions 2/3, 3/8, and 5/12 and reduce your answer to lowest terms A 10/24 C 1 11/24 B 25/24 D 1 1/2 would you add 2/24, 3/24, and 5/24 which equals 10/24 but I don't understand the lowest terms Math Help me Reduce the rational expression to lowest terms




How To Add And Subtract Square Roots 9 Steps With Pictures




What Is The Next Number In The Sequence 7 2 0 7 8 4 3 Quora
Add (2√35√2)and (√32√2) Ask questions, doubts, problems and we will help you(iii) (2 3 √ 7 − 1 2 √ 2 6 √ 11) a n d (1 3 √ 7 3 2 √ 2 − √ 11) Please scroll down to see the correct answer and solution guide Right Answer isExample 3 Adding Square Roots That Are Not Like Terms Let's say we want to add √2 and √3 Since 2 and 3 are prime numbers and share no common factors, we cannot simplify them or rewrite them in any way




How To Solve Surds 2 Four Essential Surd Techniques Suresolv




Skills 7 10 Function Notation Express The Rule In Chegg Com
4√3 2√27 =4√3 2(3√3 ) since √27 = 3√3 =4√3 6√3 =10√3;Solutions by everydaycalculationcom Answerseverydaycalculationcom » Add fractions Add 1/3 and 2/7 1 / 3 2 / 7 is 13 / 21 Steps for adding fractions Find the least common denominator or LCM of the two denominators LCM of 3 and 7 is 21 Next, find the equivalent fraction of both fractional numbers with denominator 21 For the 1st fraction, since 3 × 7 = 21, 1 / 3 = 1 × 7 / 3 × 7 Circle any terms with matching radicands Once you simplified the radicands of the terms you were given, you were left with the following equation 30√2 4√2 10√3 Since you can only add or subtract like terms, you should circle the terms that have the same radical, which in this example are 30√2 and 4√2You can think of this as being similar to adding or subtracting




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube




Square Root Of 1764 How To Find Square Root Of 1764 Solved
The prime factorization of 5 is 2•2 •3 •7•7 To be able to remove something from under the radical, there have to be 2 instances of it (because we are taking a square ie second root) √ 5 = √ 2•2 •3 •7•7 = 2 •7 •√ 3 = ± 14 • √ 3 √ 3 , rounded to 4 decimal digits, isRadicals that are "like radicals" can be added or subtracted by adding or subtracting the coefficients 1 Break down the given radicals and simplify each term 2 Identify the like radicals 3 Add or subtract the like radicals by adding or subtracting their coefficients Examples 1 4√5 3√5 2 3√75 √27 Show Stepbystep SolutionsFor example, if we add two irrational numbers, say 3 √2 4√3, a sum is an irrational number But, let us consider another example, (34√2) (4√2 ), the sum is 3, which is a rational number So, we should be very careful while adding and multiplying two irrational numbers, because it might result in an irrational number or a rational



Surds Mathematics Gcse Revision



1
It's nice to see it in geometry, rather than trying to use numbers If you have a square with sides of one unit, then the length of the diagonal is √2 (This is according to the Theorem of Pythagoras) Put two such squares together touching at one The same works with square roots For example, you can add 3√3 and 2√3 to get 5√3, in the same way that you can add 3x and 2x to get 5x You cannot, however, add 3√3 and 2√2, in the same way that you cannot add 3x and 2x2 You may, however, need to simplify the square roots before you can see whether they contain like termsThe correct dosage of adult overthecounter medicine a child can receive is given by a formula by Clark The child's weight, in pounds, is divided by 1 5 0, and the result is multi pounds lied by the adult dose of the medicineA mother need to give her daughter acetaminophen, which has an adult dose of 1 0 0 0 milligrams She does not know her daughter's exact weight, but she knows the




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Add 2 4 5 And 3 5 6 Youtube
Solve Quadratic Equation by Completing The Square 32 Solving u27u10 = 0 by Completing The Square Subtract 10 from both side of the equation u27u = 10 Now the clever bit Take the coefficient of u , which is 7 , divide by two, giving 7/2 , and finally square it giving 49/4 Add 49/4 to both sides of the equationAnswer (3) 3√3 It is an example of adding two irrational numbers 2√3 √3 We can see that there are two terms that contain two √3, one with coefficient 2 and the other with coefficient 1, and there would be 2 1 = 3 On taking out √3 as common factor √3(21) = √3(3) = 3√3 2√3 √3 = 3√3± 2 • √ 3 √ 3 , rounded to 4 decimal digits, is So now we are looking at x = ( 2 ± 2 • 1732 ) / 4 Two real solutions x =(2√ 12)/4=(1√ 3 )/2= 0366 or x =(2√ 12)/4=(1√ 3 )/2= 1366 Solving a Single Variable Equation 45 Solve x2 = 0 Add 2 to both sides of the equation x = 2 Three solutions were




How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com




Lesson 4 Operations With Radicals 0
3•3 •3•3 To be able to remove something from under the radical, there have to be 2 instances of it (because we are taking a square ie second root) √ 81 = √ 3•3 •3•3 = 3 •3 •√ 1 = Transcript Example 13 Add 2 √2 5 √3 and √2 3 √3 Here, both numbers have root in it So, we combine the numbers with the same root Combining 2 √2 & √2 and 5√3 & 3 √3, and then solving 2 √2 5 √3 √2 – 3 √3 = (2 √2 √2) (5√3 – 3 √3) = √2 (2 1) √3(5 – 3) = 3 √2 2X = 5 1 1 4 i ≈ 0 2 0 7 4 8 3 3 1 4 7 7 i x = 5 − 1 4 i 1 ≈ 0 2 − 0 7 4 8 3 3 1 4 7 7 i Steps Using the Quadratic Formula Steps for Completing the Square




If 5 2 Root 3 7 4 Root 3 A B Root 3 Find A And B Brainly In



What Is The Answer Of Simplify 7 3 5 3 5 7 3 5 3 5 Quora
Variable x cannot be equal to any of the values 2,3 since division by zero is not defined Multiply both sides of the equation by \left(x3\right)\left(x2\right), the least common multiple of x2,x3The reason is that if we need to add or subtract fractions with radicals, it's easier to compute if1 2sqrt(2)1/ 2sqrt2 First multiply bu sqrt(2) ==> 2sqrt(2)*sqrt2 1*sqrt2/2sqrt2*sqrt2 ==> (2*2 sqrt2)/2*2 ==> (4sqrt2)/4 ==> 1sqrt2/4 2 3sqrt2 2sqrt3




Simplify 5 3 7 4 3 5 3 7 4 3 Brainly In



1
Correct answers 1 question Add 2√2 5√3 and √2 3√2Now, applying the Square Root Principle to Eq #741 we get x2 = √ 5 Add 2 to both sides to obtain x = 2 √ 5 Since a square root has two values, one positive and the other negative x 2 4x 1 = 0 has two solutions x = 2 √ 5 or x = 2 √ 5 Solve Why is (2 √3) / 3 the simpler form of 2 / √3 ?




Multiplying And Dividing Radical Expressions



Problem Solving If 3 2 7 5 4 23 7 6 47 And 9 8 79 To What Is 10 9 Equal Quora
Math Secondary School answer answered Add 2√2 5√3 and√2 3√3 2 See answers report flag outlinedQuestion 1Simplify√(8y^7 )Assume That The Variable Represents A Positive Number2 Simplify√18 Z√5 0z Assume That The Variable Represents A Positive Real Number3 Simplify√(2u^3 ) V^(4 ) √(8u^4 V)Assume That The Variable Represents Positive Real Number4 Add (22i)(64ⅈ)Write Your Answer As A Complex Number In Standard Form53x22x2=4 Two solutions were found x =(2√76)/6=(1√ 19 )/3= 11 x =(2√76)/6=(1√ 19 )/3= 1786 Rearrange Rearrange the equation by subtracting what is to the right of the equal sign




Addition Wikipedia




Solved Add 5 Root 3 2 Root 7 2 Root 3 Root 5 Brainly In
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Numbers In Python Real Python




True Or False Nz Maths



What Is 2 5 3 7



Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian




Addition Sums Up To Free Printable Worksheets Worksheetfun
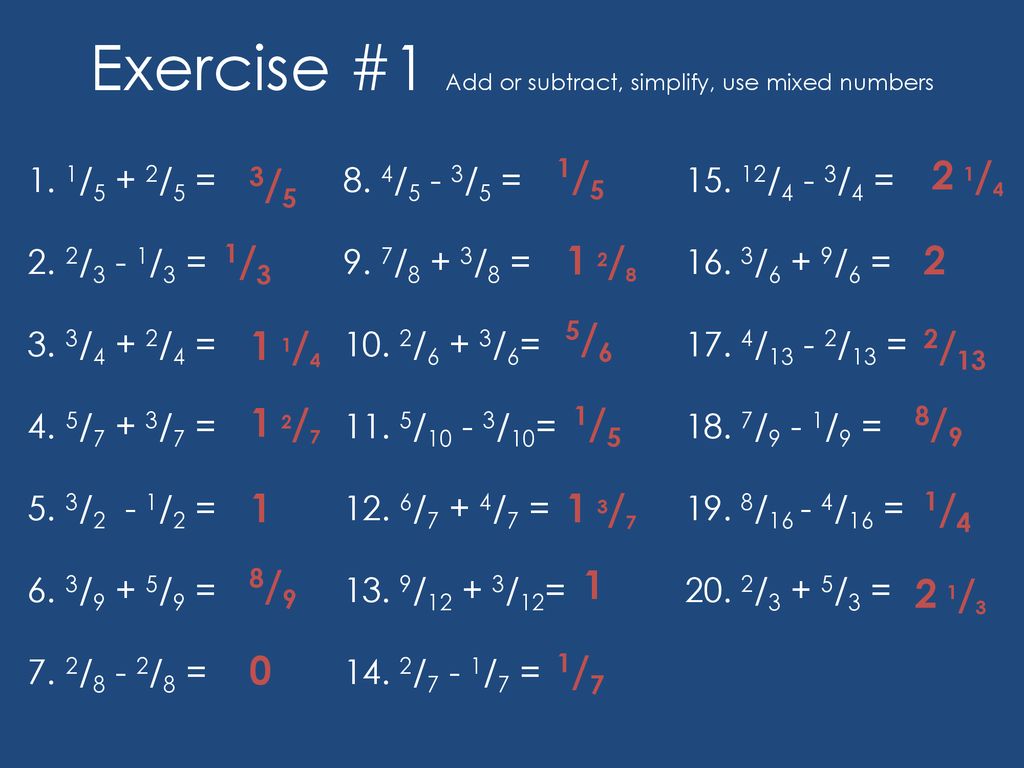



Adding And Subtracting Fractions Ppt Download




Adding And Subtracting With Integers Integers Siyavula
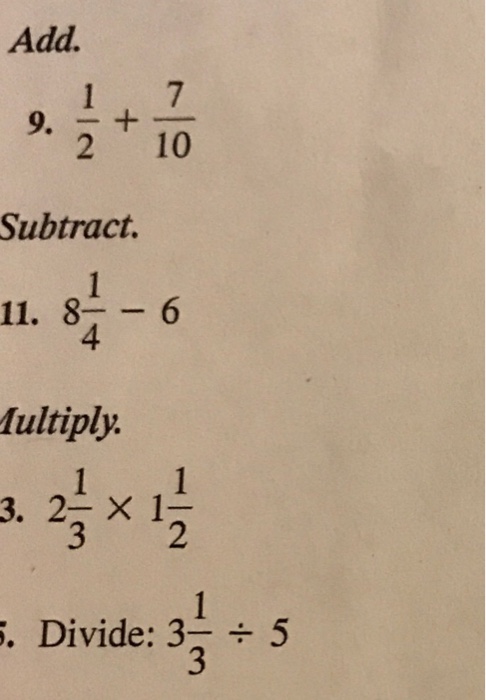



Add 1 2 7 10 Subtract 8 1 4 6 Multiply 2 Chegg Com




Why Square Root 7 Power 1 1




Multiplying And Dividing Radical Expressions




Simplify Simplify Radical Rational Expression With Step By Step Math Problem Solver
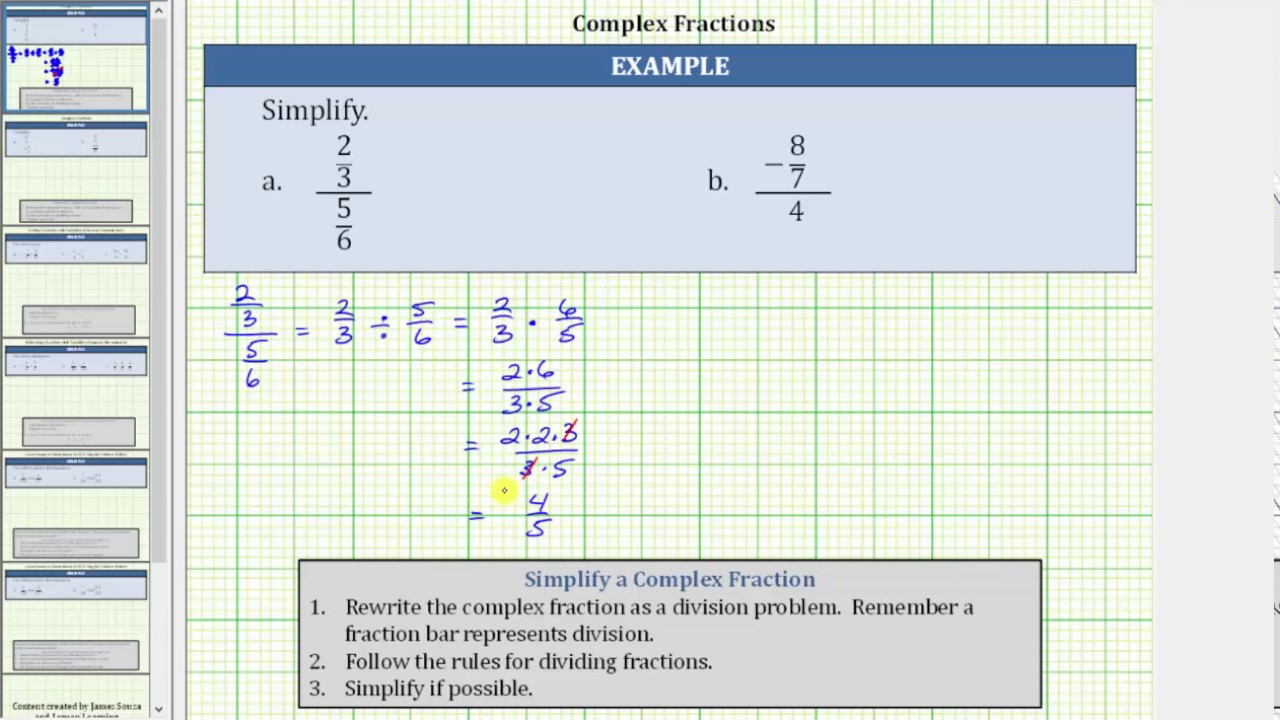



Simplify Complex Fractions 2 3 5 6 And 8 7 4 Youtube




Proof 2 Is Irrational Algebra Video Khan Academy




3 Number What Is There To Know Adding It Up Helping Children Learn Mathematics The National Academies Press



3 Number What Is There To Know Adding It Up Helping Children Learn Mathematics The National Academies Press




Ex 7 6 1 Solve A 2 3 1 7 B 3 10 7 15 C 4 9 2 7 D 5 7



Adding Subtracting Radicals Square Roots Purplemath



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Adding And Subtracting Negative Numbers Worksheets



Numbers Are All Around You We Can Use Numbers In Our Everyday Life To Re Write Them In Simplified Radical Form You Will Add Numbers That Are Course Hero




5 2 3 7 4 3 A B 3 Find The Value Of A And B Of The Following Brainly In




The Symbol Means Radical Or Square Root A X2 2x




Magic Numbers Numbers Teaching Mathematics




Adding Square Roots Study Com




Multiply 3 Root 5 By 2 Root 6 Root 15 By 4 Root 5 2 Root 6 By 3 Root 3 3 Root 8 By 3 Root 2 Youtube




Add 2 Root 2 5 Root 3 And Root 2 3 Root 3 Youtube




Add 2 3 Root 7 1 2 Root 2 6 Root 11 And 1 3 Root 7 3 2 Root 2 Root 11 Brainly In




Simplifying Square Root Expressions Video Khan Academy




1 Express The Following Rule In Function Notation Chegg Com
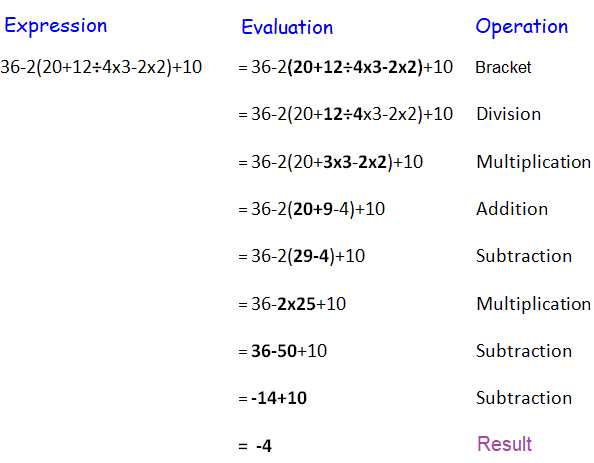



Bodmas Rule



Http Zimmer Csufresno Edu Kbyler Archive 08 2 M75a Exam 75amt1prac Pdf



1




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising
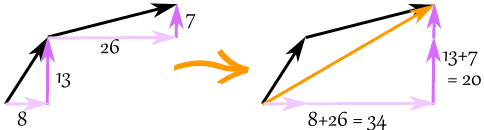



Add The Vectors




Put Any Mathematical Sign Puzzle Answers With Full Solutions Inside



Solve Equations With Square Roots Elementary Algebra
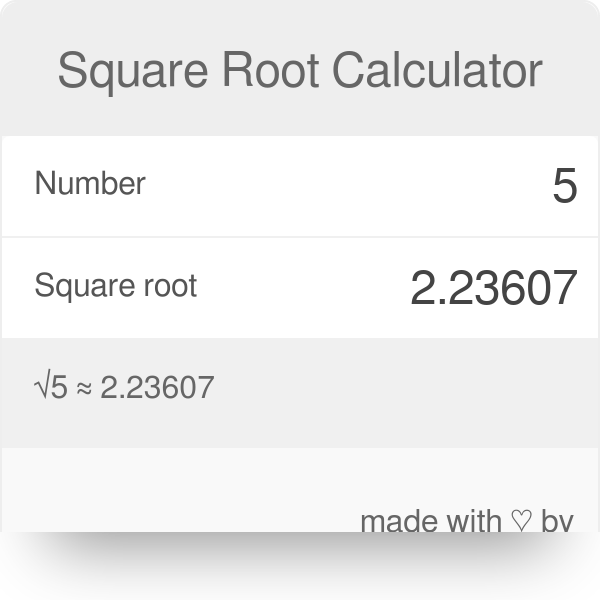



Square Root Calculator Find The Square Root In One Easy Step




Square Root Of 294 How To Find Square Root Of 294 Solved



Problem Solving If 3 2 7 5 4 23 7 6 47 And 9 8 79 To What Is 10 9 Equal Quora




Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver




How To Add And Subtract Square Roots 9 Steps With Pictures




Wolfram Alpha Examples Step By Step Solutions




On Adding 2 3 And 3 2 We Get Maths Number Systems Meritnation Com




Add 3 2 7 3 And 2 5 3 Brainly In



What Is The Answer Of Simplify 7 3 5 3 5 7 3 5 3 5 Quora




How To Add And Subtract Square Roots 9 Steps With Pictures




Simplify Add Or Subtract Fractions With Step By Step Math Problem Solver
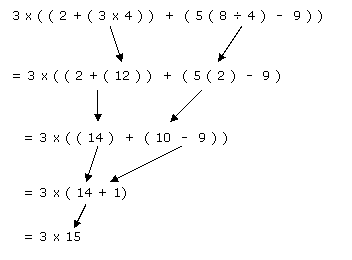



Order Of Operations




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Real Numbers Geeksforgeeks
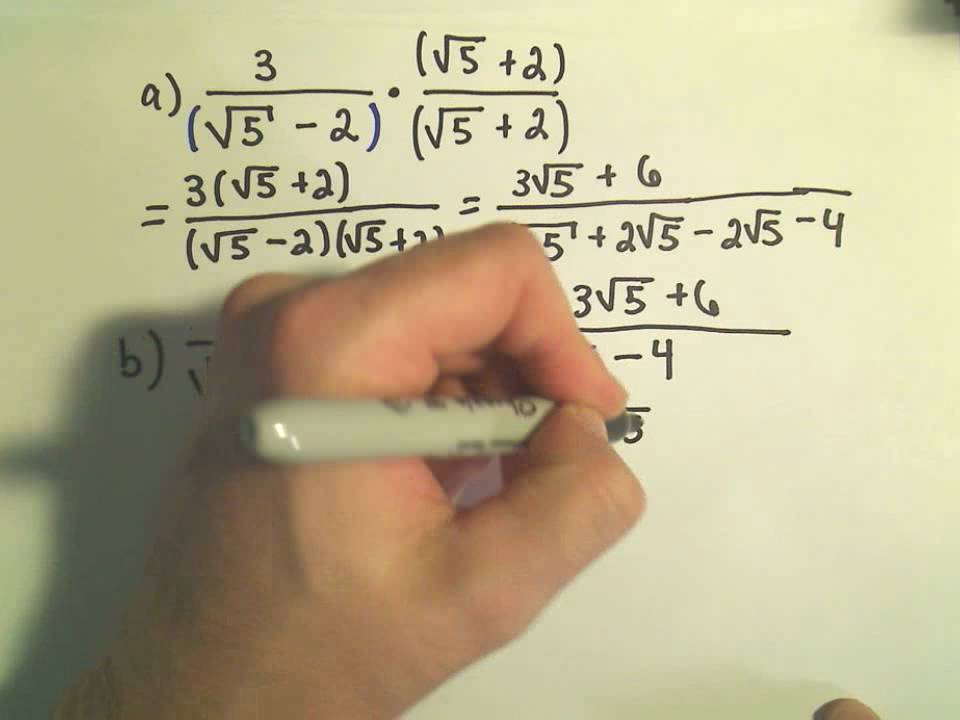



Rationalizing The Denominator Example 1 Youtube



What Is 2 5 3 7



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline



Python Challenges 1 Exercises Practice Solution W3resource



Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra




Rd Sharma Class 9 Solutions Maths Chapter 3 Rationalisation Updated For 21 22



If A 1 7 4 3 And B 1 7 4 3 Then Find The Value Of Studyrankersonline




Add 2 3 5 5 7 7 And 3 5 3 7 Brainly In




Add 3 2 7 3 And 2 5 3 Brainly In




How To Add And Subtract Square Roots 9 Steps With Pictures




Add 2 4 5 And 3 5 6 Youtube




Add 3 2 7 3 And 2 5 3 Rational Numbers Video Teachoo



1




How To Add And Subtract Square Roots 9 Steps With Pictures




Confidential 1 Algebra1 Adding And Subtracting Radical Expressions Ppt Download



Danville Edu Sites Default Files Assets Files Math lab Solving exponential equations Pdf



What Is 2 7 2 3




4 4 3 2 5 5 7 2 1 9 3 12 4 6 28 21 12 Gauthmath




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Find The Values Of A And B If 7 3 5 3 5 7 3 5 3 5




Operations On Radical Expressions Beginning Algebra




Simplifying Radical Expressions




Ex 6 1 7 Without Adding Find The Sum I 1 3 5 7 9




4 Square Root Of 3 5 Square Root Of 2 2 Square Gauthmath




Simplifying Square Root Expressions No Variables Video Khan Academy
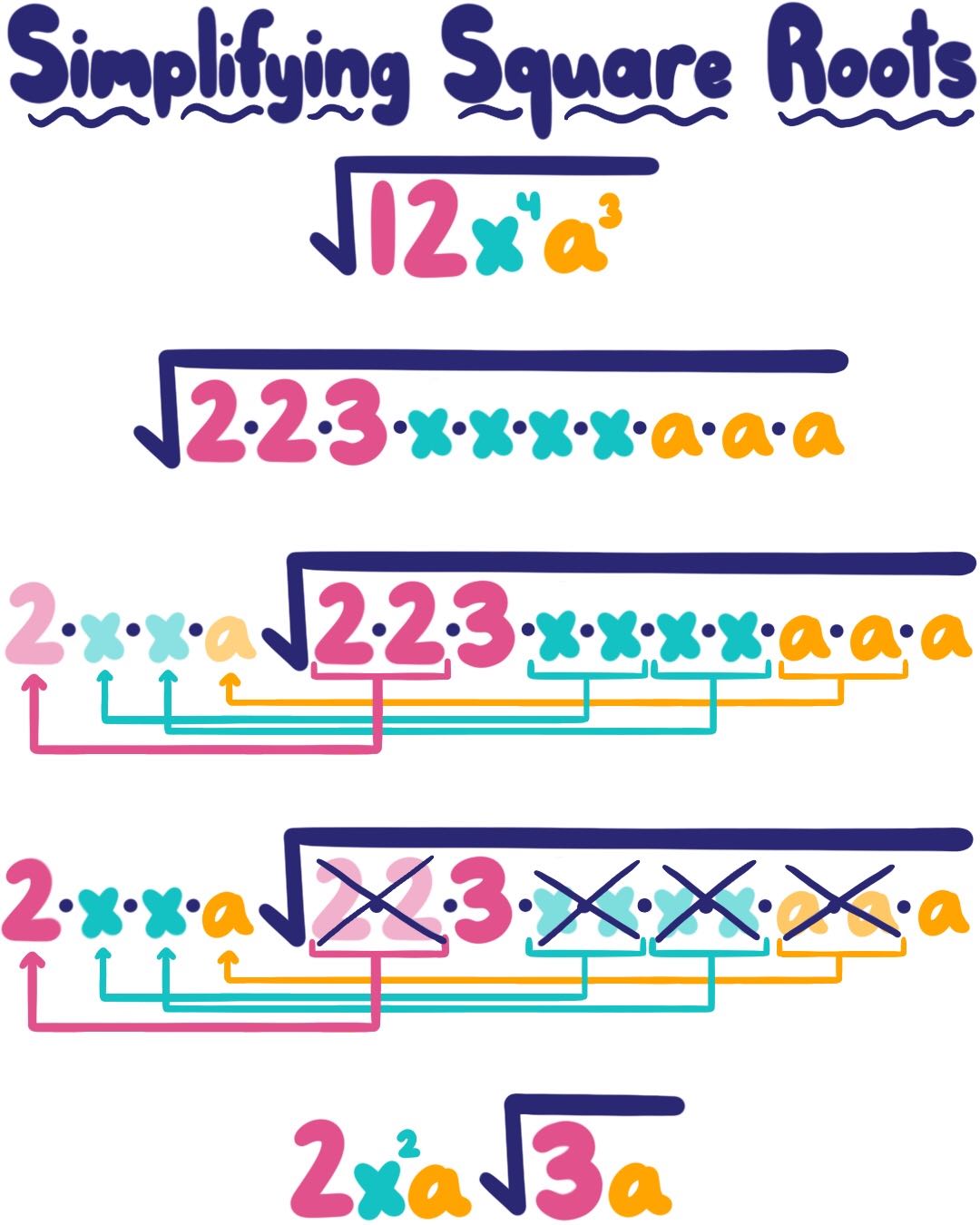



Simplifying Square Roots Examples Practice Expii




To Calculate The Standard Deviation Of Those Numbers Chegg Com



C Program To Add Two Arrays




The Value Of 3 1 2 2 2 5 2 2 3 2 7 3 2 4 2 9 4 2 5 2 11 5 2 6 2 13 6 2 7 2 15 7 2 8 2 17 8 2 9 2 19 9 2 10 2 Is 1 100 B 99 100 C 1 D 101 100




Math Tricks Explained The New York Times




Add 2 5 5 7 3 10 1 5 Mathematics Topperlearning Com Ewwxcpjj




Skills 7 10 Function Notation Express The Rule In Chegg Com



0 件のコメント:
コメントを投稿