円周と円周率 面積 表面積 体積の求め方について基本を解説 高校生向け受験応援メディア 受験のミカタ
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学5年生の算数 体積 直方体と立方体の体積面積と体積1 / 2 4pm 平成16 年1 月21 日Uryu Hitoshi 面積と体積 1 Graminan n 次元実ベクトル空間にベクトルa1,a2,··,am ∈ Rn がある。 ただし、 0 ≤ m ≤ n とする。 行列Am = (a1,a2,··,am) と行列Gm = ((ai,aj)) (0 ≤ i,j ≤ m) を考える。ここでGm はグラムの行列と呼ばれている。Gm の行列式detGm
面積と体積の問題
面積と体積の問題-角錐台の体積 角錐台の体積 角錐台の底面積と上面積と高さから体積を計算します。 角錐の体積 角錐の体積 角錐の底面積と高さから体積を計算します。 直円柱の体積 直円柱の体積 直円柱の半径と高さから体積、側面積、表面積を計算します。2角柱と円柱 角柱・円柱の体積＝底面積×高さ 角柱・円柱の表面積＝底面積×2側面積 3角すいと円すい
目で見る数学の基礎 面積と体積 大野 栄一 本 通販 Amazon
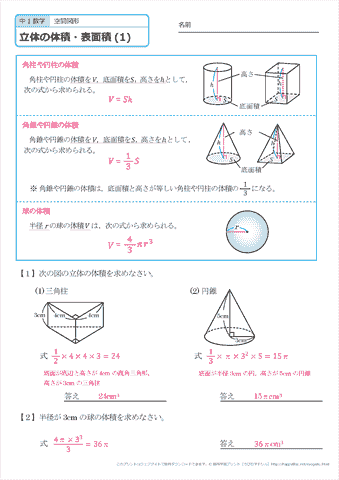
体積 = 底面積 × 高さ 円柱の体積 半径 r、高さ h の 円柱 えんちゅう 円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。 円柱 えんちゅう の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 どうしゅつ 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 錐体の体 まず、「 柱」の体積の求め方を確認しましょう。 （ 柱の体積） ＝ （底面積） × （高さ） でしたね。 円柱の底面は「円」ですから、 （円柱の体積） ＝ （底面の円の面積） × （高さ） ですね。 では、「円の面積の求め方」も確認しましょう。 これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 （円の面積） ＝ （半径） × （半径） × （円周率π） ですね 表面積と体積の質問なんですが。 異なる形状で表面積が同じ場合、体積も同じになるでしょうか？ 同じような気がするのですが 確信が持てないのと 例外的な場合がありそうで質問をさせて頂きました。 どうぞ、よろしくお願 いいたします。
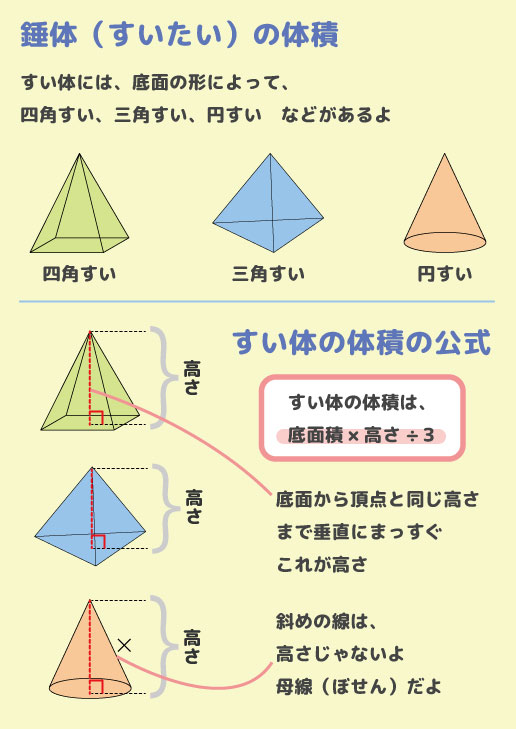
解（錐体の体積）＝ 1 3 ×（底面積）×（高さ）より， 1 3 ×（∏×32）×6＝18∏ （cm3） 答18∏cm3 ① （錐体の表面積）＝（側面積）＋（底面積） ② 円錐の底面の周の長さ（側面の扇形の弧の長さ）を¬，母線の長さをR，側面積をSとすると， S＝ 1 2 ¬R ③ 円錐の底面の半径をrとすると，②より，S＝ 1 2 ×2∏r×R，すなわち，S＝∏rR ④ 側面の扇形の中心角は， r R ×360° 問題2右の図の円錐の表面積相似比（辺の長さの比）から 面積比 と 体積比 を求めましょう。 長さ $2\rm cm$ と $3\rm cm$ の辺があります。この $2$ 辺の長さの比 （相似比）は $\textcolor{blue}{23}$ になります。 正方形にしてそれぞれの面積を考えると、 $1$ 辺の長さが $2 \rm cm2×2（2\textcolor{blue} 体積やかさは、なかなかに難しい単元です。 面積や長さはまだ紙の上には書くことができても、立体となるとそうもいきません。 体積やかさに関する記事を集めました。 かさ・体積・容積のまとめ 小学2年生に体積・かさの単位変換をマ
面積と体積の問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 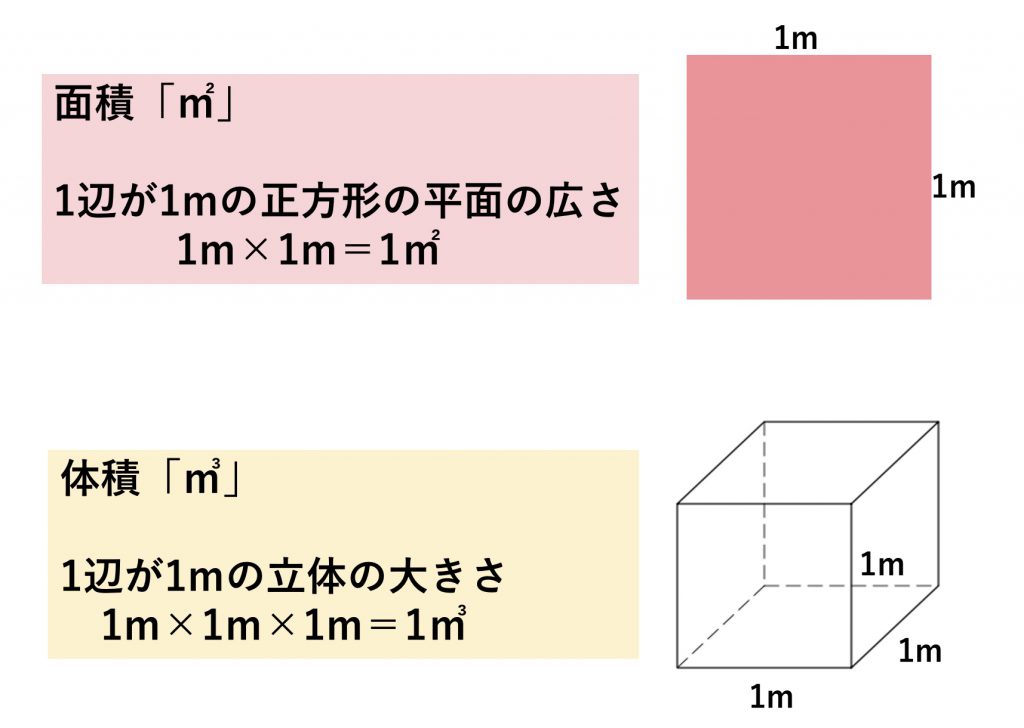 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 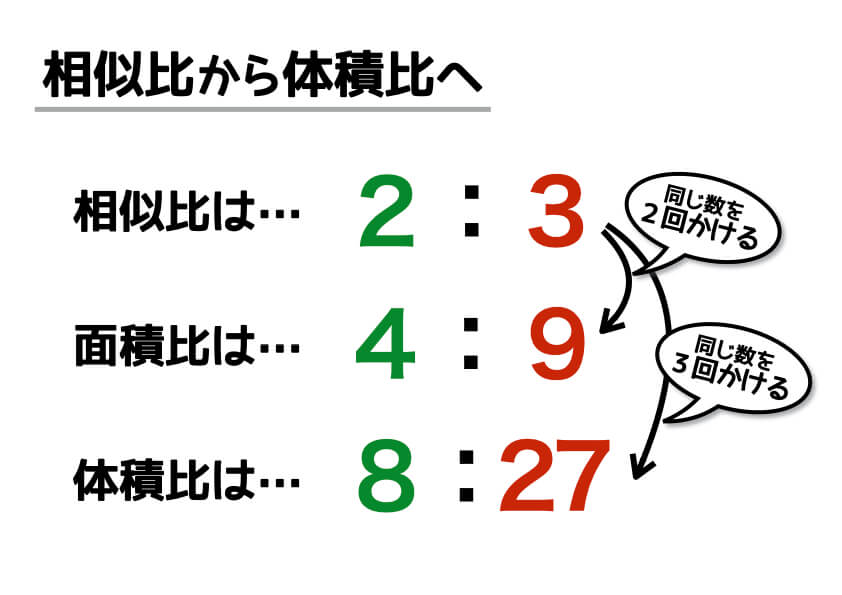 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 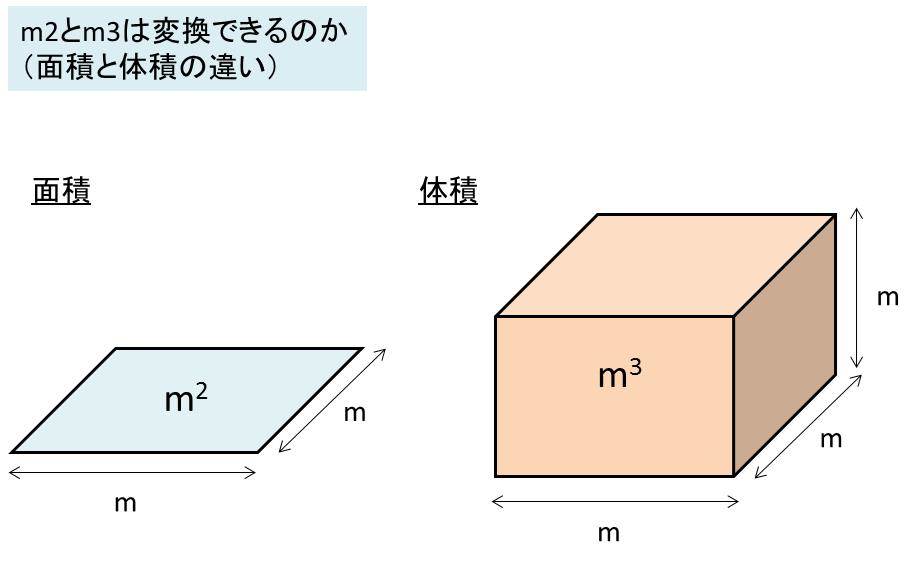 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
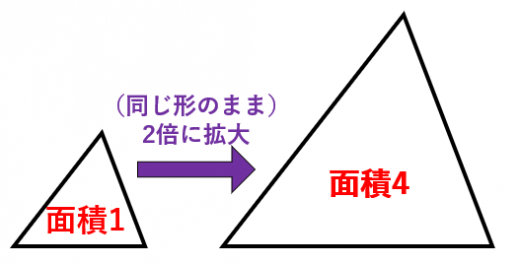 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |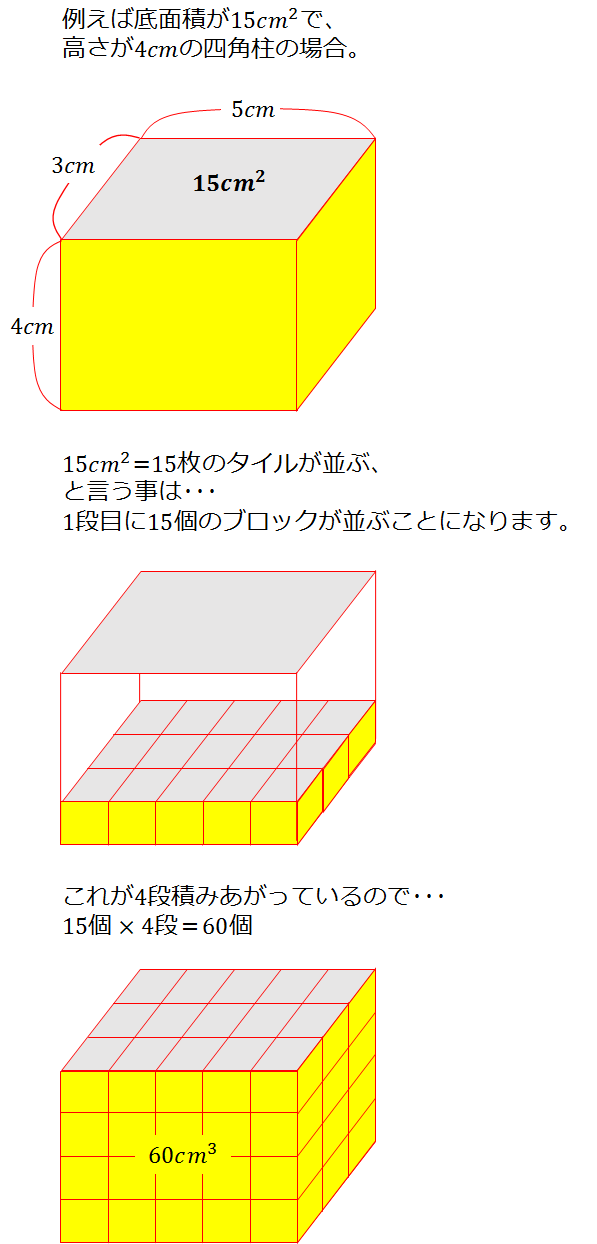
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 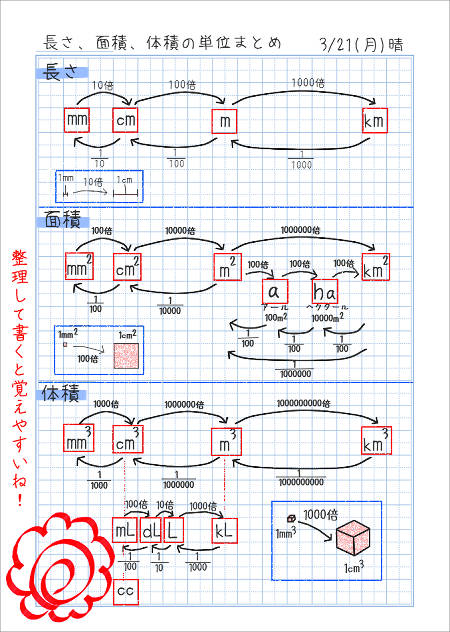 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 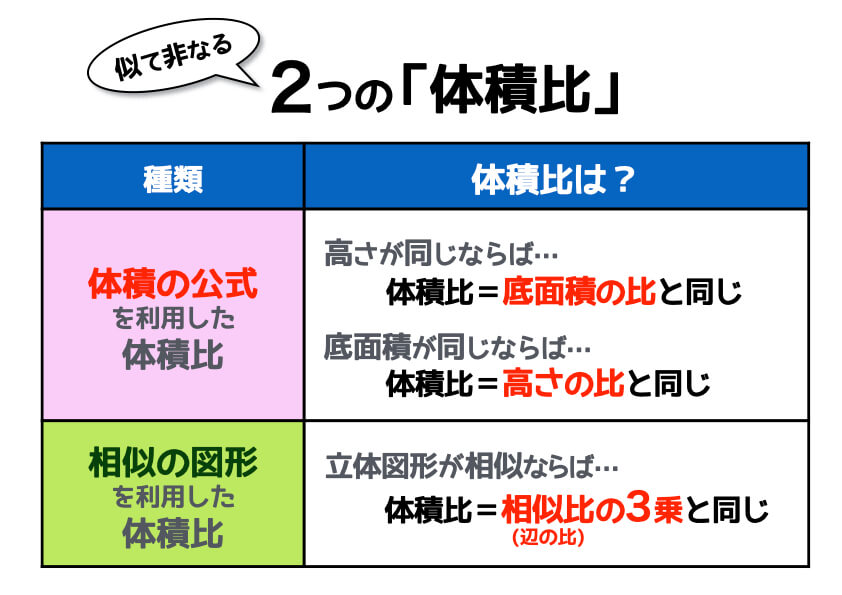 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 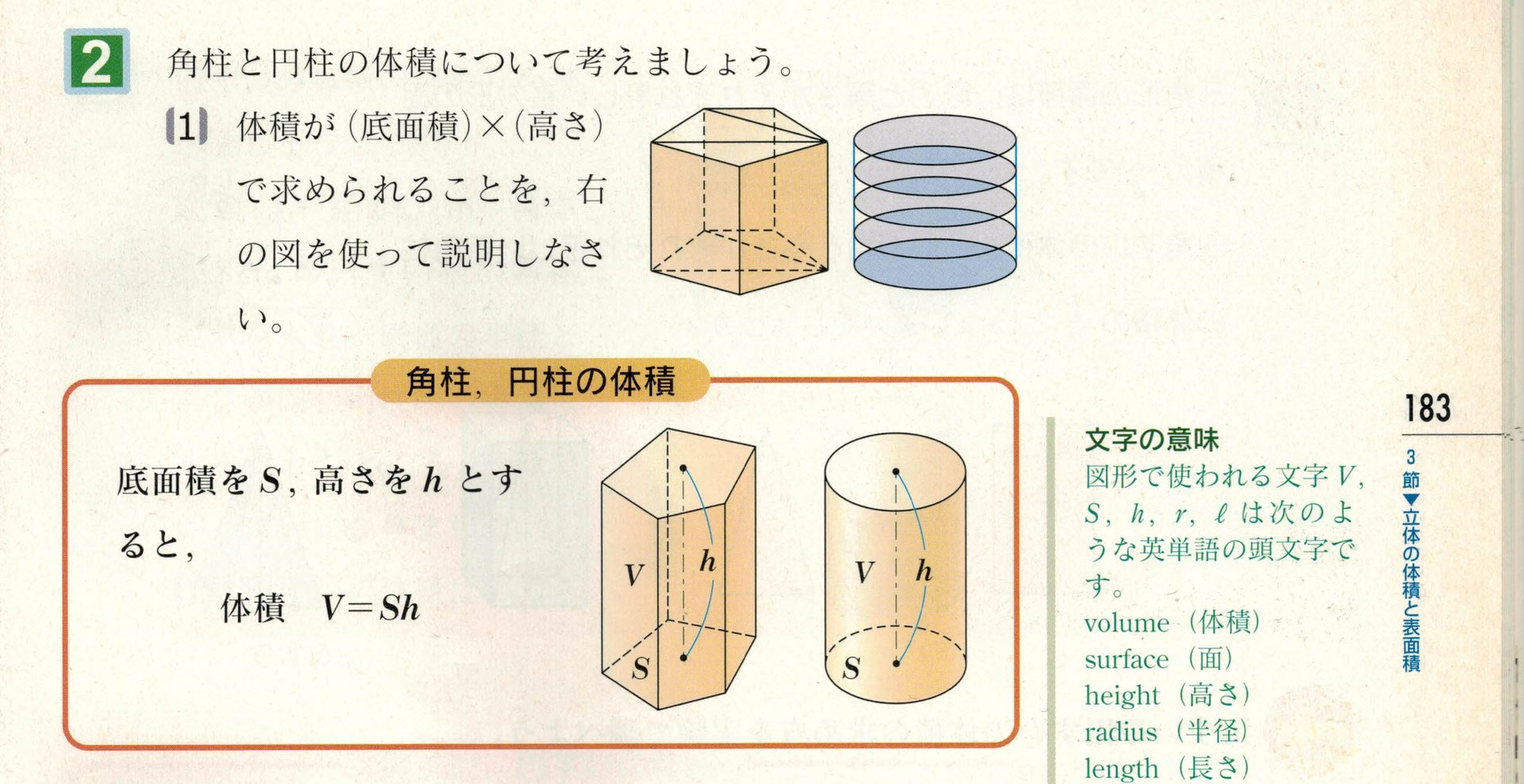 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 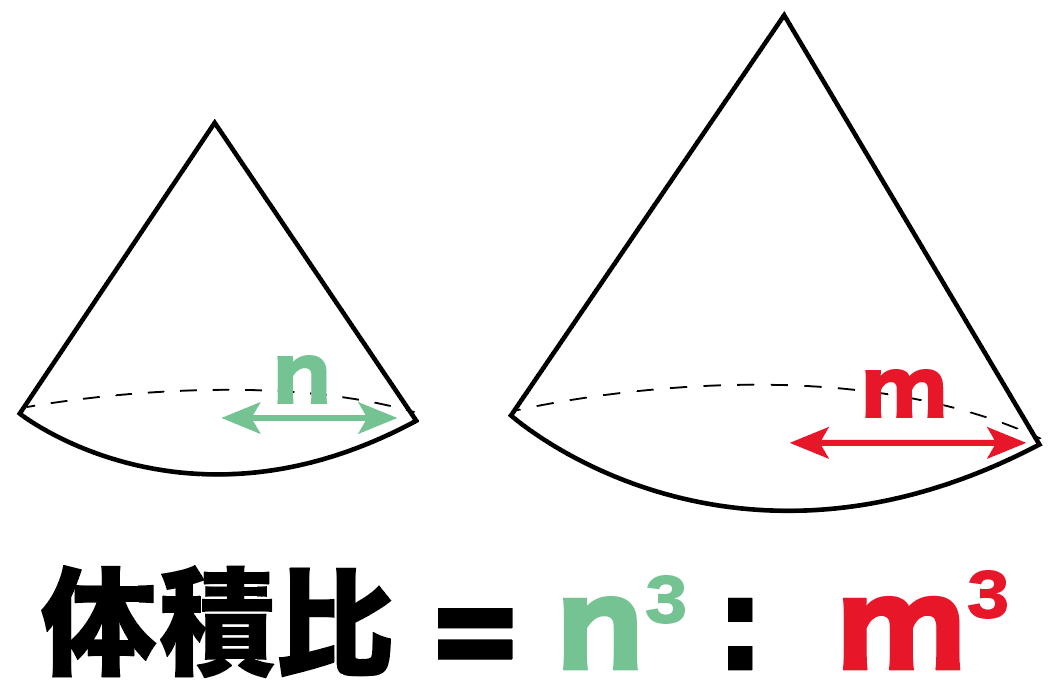 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 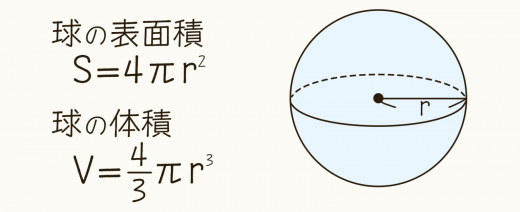 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 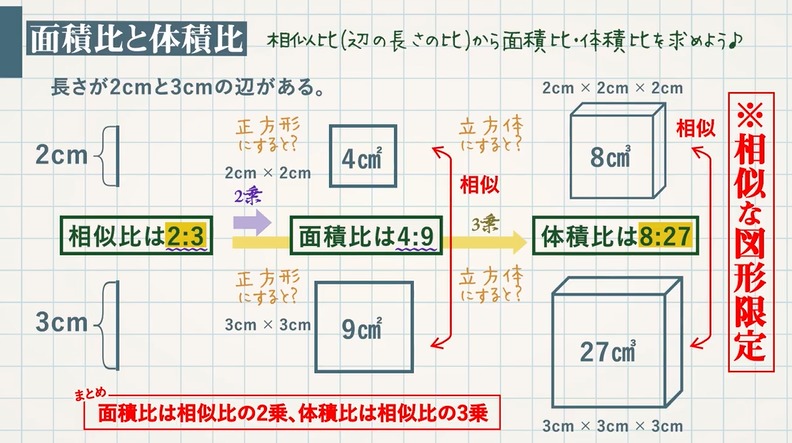 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 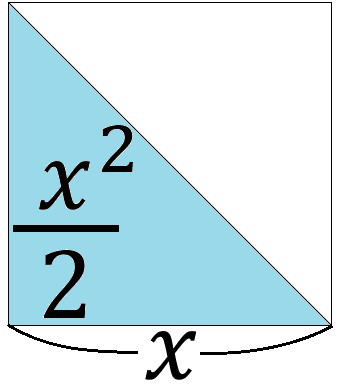 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 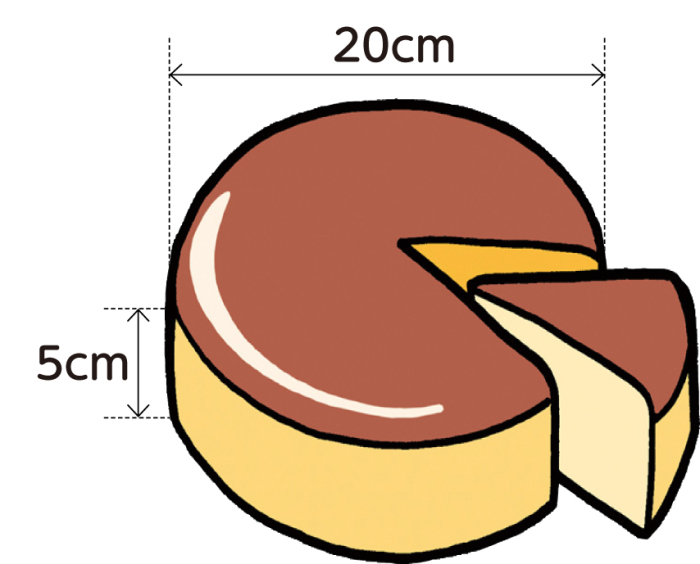 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 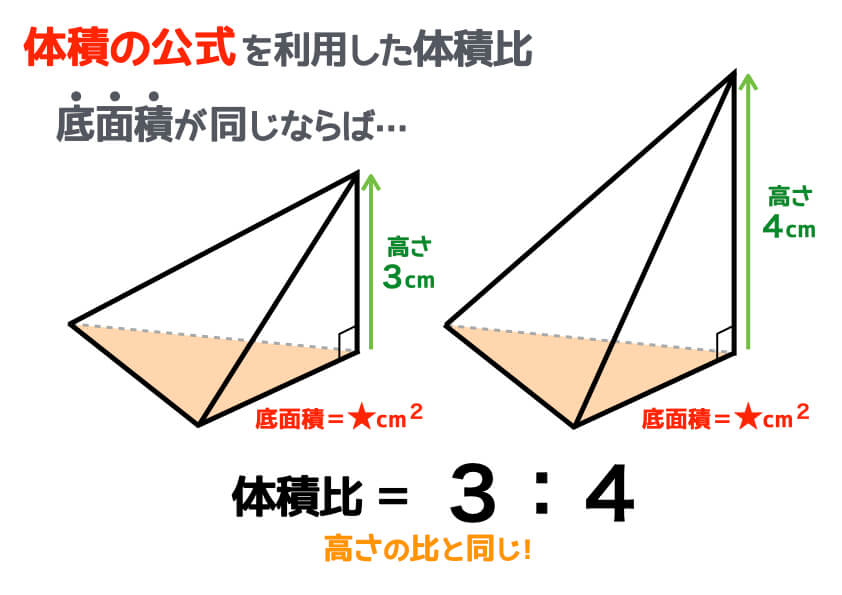 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
「面積と体積の問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 | 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
 図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |  図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 |
角柱と円柱の体積 = = 底面積× × 高さ 角錐と円錐の体積 = = 底面積× × 高さ× 1 3 × 1 3 球の半径をrとすると、球の体積 = = 4 3πr³ 4 3 π r ³ 意味を理解したら問題を解いてみましょう。 各図形の体積を求めなさい。 答えはこちらをクリック 円柱の体積は 3 柱の体積 = 底面積 × 高さ 表面積 = 底面積 × 2 側面積 円周や側面積とかの求め方も知りたいっピ わかりました。 他に知っておくべき公式は ・ 円周 = 直径 × 314 (π) ・ 側面積 = 底面の周 × 高さ ・ 円の面積 = 半径 × 半径 × 314 (π) ですね。 練習問題 （1）次の円柱の体積と表面積を求めなさい。 ただし、円周率はπとする。 答え&解説 （2）次の三角柱の体積と表面積を求めなさい
Incoming Term: 面積と体積, 面積と体積の違い, 面積と体積の関係, 面積と体積の求め方, 面積と体積の公式, 面積と体積の問題, 面積と体積の単位, 面積と体積の計算法, 面積と体積の関係 換算,
0 件のコメント:
コメントを投稿